Dfyjkt

Laser light is a type of stimulated emission of radiation.

Stimulated emission is the process by which an incoming photon of a specific frequency can interact with an excited atomic electron (or other excited molecular state), causing it to drop to a lower energy level. The liberated energy transfers to the electromagnetic field, creating a new photon with a phase, frequency, polarization, and direction of travel that are all identical to the photons of the incident wave. This is in contrast to spontaneous emission, which occurs at random intervals without regard to the ambient electromagnetic field.

The process is identical in form to atomic absorption in which the energy of an absorbed photon causes an identical but opposite atomic transition: from the lower level to a higher energy level. In normal media at thermal equilibrium, absorption exceeds stimulated emission because there are more electrons in the lower energy states than in the higher energy states. However, when a population inversion is present, the rate of stimulated emission exceeds that of absorption, and a net optical amplification can be achieved. Such a gain medium, along with an optical resonator, is at the heart of a laser or maser.
Lacking a feedback mechanism, laser amplifiers and superluminescent sources also function on the basis of stimulated emission.

Overview

Electrons and their interactions with electromagnetic fields are important in our understanding of chemistry and physics.
In the classical view, the energy of an electron orbiting an atomic nucleus is larger for orbits further from the nucleus of an atom. However, quantum mechanical effects force electrons to take on discrete positions in orbitals. Thus, electrons are found in specific energy levels of an atom, two of which are shown below:

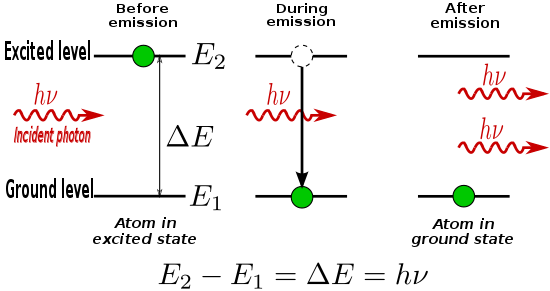
When an electron absorbs energy either from light (photons) or heat (phonons), it receives that incident quantum of energy. But transitions are only allowed between discrete energy levels such as the two shown above.
This leads to emission lines and absorption lines.

When an electron is excited from a lower to a higher energy level, it unlikely for it to stay that way forever.
An electron in an excited state may decay to a lower energy state which is not occupied, according to a particular time constant characterizing that transition. When such an electron decays without external influence, emitting a photon, that is called "spontaneous emission". The phase and direction associated with the photon that is emitted is random. A material with many atoms in such an excited state may thus result in radiation which has a narrow spectrum (centered around one wavelength of light), but the individual photons would have no common phase relationship and would also emanate in random directions. This is the mechanism of fluorescence and thermal emission.

An external electromagnetic field at a frequency associated with a transition can affect the quantum mechanical state of the atom without being absorbed. As the electron in the atom makes a transition between two stationary states (neither of which shows a dipole field), it enters a transition state which does have a dipole field, and which acts like a small electric dipole, and this dipole oscillates at a characteristic frequency. In response to the external electric field at this frequency, the probability of the electron entering this transition state is greatly increased. Thus, the rate of transitions between two stationary states is increased beyond that of spontaneous emission. A transition from the higher to a lower energy state produces an additional photon with the same phase and direction as the incident photon; this is the process of stimulated emission.

History

Stimulated emission was a theoretical discovery by Einstein^[1][2] within the framework of the old quantum theory, wherein the emission is described in terms of photons that are the quanta of the EM field. Stimulated emission can also occur in classical models, without reference to photons or quantum-mechanics.^[3] (See also Laser#history.)

Mathematical model

Stimulated emission can be modelled mathematically by considering an atom that may be in one of two electronic energy states, a lower level state (possibly the ground state) (1) and an excited state (2), with energies E₁ and E₂ respectively.

If the atom is in the excited state, it may decay into the lower state by the process of spontaneous emission, releasing the difference in energies between the two states as a photon. The photon will have frequency ν₀ and energy hν₀, given by:

E2−E1=hν0displaystyle E_2-E_1=h,nu _0

where h is Planck's constant.

Alternatively, if the excited-state atom is perturbed by an electric field of frequency ν₀, it may emit an additional photon of the same frequency and in phase, thus augmenting the external field, leaving the atom in the lower energy state. This process is known as stimulated emission.

In a group of such atoms, if the number of atoms in the excited state is given by N₂, the rate at which stimulated emission occurs is given by

∂N2∂t=−∂N1∂t=−B21ρ(ν)N2displaystyle frac partial N_2partial t=-frac partial N_1partial t=-B_21,rho (nu ),N_2

where the proportionality constant B₂₁ is known as the Einstein B coefficient for that particular transition, and ρ(ν) is the radiation density of the incident field at frequency ν. The rate of emission is thus proportional to the number of atoms in the excited state N₂, and to the density of incident photons.

At the same time, there will be a process of atomic absorption which removes energy from the field while raising electrons from the lower state to the upper state. Its rate is given by an essentially identical equation,

∂N2∂t=−∂N1∂t=B12ρ(ν)N1displaystyle frac partial N_2partial t=-frac partial N_1partial t=B_12,rho (nu ),N_1.

The rate of absorption is thus proportional to the number of atoms in the lower state, N₁. Einstein showed that the coefficient for this transition must be identical to that for stimulated emission:

B12=B21displaystyle B_12=B_21.

Thus absorption and stimulated emission are reverse processes proceeding at somewhat different rates. Another way of viewing this is to look at the net stimulated emission or absorption viewing it as a single process. The net rate of transitions from E₂ to E₁ due to this combined process can be found by adding their respective rates, given above:

∂N1net∂t=−∂N2net∂t=B21ρ(ν)(N2−N1)=B21ρ(ν)ΔNdisplaystyle frac partial N_1^textnetpartial t=-frac partial N_2^textnetpartial t=B_21,rho (nu ),(N_2-N_1)=B_21,rho (nu ),Delta N.

Thus a net power is released into the electric field equal to the photon energy hν times this net transition rate. In order for this to be a positive number, indicating net stimulated emission, there must be more atoms in the excited state than in the lower level: ΔN>0displaystyle Delta N>0. Otherwise there is net absorption and the power of the wave is reduced during passage through the medium. The special condition N2>N1displaystyle N_2>N_1 is known as a population inversion, a rather unusual condition that must be effected in the gain medium of a laser.

The notable characteristic of stimulated emission compared to everyday light sources (which depend on spontaneous emission) is that the emitted photons have the same frequency, phase, polarization, and direction of propagation as the incident photons. The photons involved are thus mutually coherent. When a population inversion (ΔN>0displaystyle Delta N>0) is present, therefore, optical amplification of incident radiation will take place.

Although energy generated by stimulated emission is always at the exact frequency of the field which has stimulated it, the above rate equation refers only to excitation at the particular optical frequency ν0displaystyle nu _0 corresponding to the energy of the transition. At frequencies offset from ν0displaystyle nu _0 the strength of stimulated (or spontaneous) emission will be decreased according to the so-called line shape.
Considering only homogeneous broadening affecting an atomic or molecular resonance, the spectral line shape function is described as a Lorentzian distribution

g′(ν)=1π(Γ/2)(ν−ν0)2+(Γ/2)2displaystyle g'(nu )=1 over pi (Gamma /2) over (nu -nu _0)^2+(Gamma /2)^2

where Γdisplaystyle Gamma , is the full width at half maximum or FWHM bandwidth.

The peak value of the Lorentzian line shape occurs at the line center, ν=ν0displaystyle nu =nu _0. A line shape function can be normalized so that its value at ν0displaystyle nu _0 is unity; in the case of a Lorentzian we obtain

g(ν)=g′(ν)g′(ν0)=(Γ/2)2(ν−ν0)2+(Γ/2)2displaystyle g(nu )=g'(nu ) over g'(nu _0)=(Gamma /2)^2 over (nu -nu _0)^2+(Gamma /2)^2.

Thus stimulated emission at frequencies away from ν0displaystyle nu _0 is reduced by this factor. In practice there may also be broadening of the line shape due to inhomogeneous broadening, most notably due to the Doppler effect resulting from the distribution of velocities in a gas at a certain temperature. This has a Gaussian shape and reduces the peak strength of the line shape function. In a practical problem the full line shape function can be computed through a convolution of the individual line shape functions involved. Therefore, optical amplification will add power to an incident optical field at frequency νdisplaystyle nu at a rate given by

P=hνg(ν)B21ρ(ν)ΔNdisplaystyle P=hnu ,g(nu ),B_21,rho (nu ),Delta N.

Stimulated emission cross section

The stimulated emission cross section is

σ21(ν)=A21λ28πn2g(ν)displaystyle sigma _21(nu )=A_21frac lambda ^28pi n^2g(nu )

where

A₂₁ is the Einstein A coefficient,

λ is the wavelength in vacuum,

n is the refractive index of the medium (dimensionless), and

g(ν) is the spectral line shape function.

Optical amplification

Stimulated emission can provide a physical mechanism for optical amplification. If an external source of energy stimulates more than 50% of the atoms in the ground state to transition into the excited state, then what is called a population inversion is created. When light of the appropriate frequency passes through the inverted medium, the photons are either absorbed by the atoms that remain in the ground state or the photons stimulate the excited atoms to emit additional photons of the same frequency, phase, and direction. Since more atoms are in the excited state than in the ground state then an amplification of the input intensity results.

The population inversion, in units of atoms per cubic meter, is

ΔN21=N2−g2g1N1displaystyle Delta N_21=N_2-g_2 over g_1N_1

where g₁ and g₂ are the degeneracies of energy levels 1 and 2, respectively.

Small signal gain equation

The intensity (in watts per square meter) of the stimulated emission is governed by the following differential equation:

dIdz=σ21(ν)⋅ΔN21⋅I(z)displaystyle dI over dz=sigma _21(nu )cdot Delta N_21cdot I(z)

as long as the intensity I(z) is small enough so that it does not have a significant effect on the magnitude of the population inversion. Grouping the first two factors together, this equation simplifies as

dIdz=γ0(ν)⋅I(z)displaystyle dI over dz=gamma _0(nu )cdot I(z)

where

γ0(ν)=σ21(ν)⋅ΔN21displaystyle gamma _0(nu )=sigma _21(nu )cdot Delta N_21

is the small-signal gain coefficient (in units of radians per meter). We can solve the differential equation using separation of variables:

dII(z)=γ0(ν)⋅dzdisplaystyle dI over I(z)=gamma _0(nu )cdot dz

Integrating, we find:

ln⁡(I(z)Iin)=γ0(ν)⋅zdisplaystyle ln left(I(z) over I_inright)=gamma _0(nu )cdot z

or

I(z)=Iineγ0(ν)zdisplaystyle I(z)=I_ine^gamma _0(nu )z

where

Iin=I(z=0)displaystyle I_in=I(z=0), is the optical intensity of the input signal (in watts per square meter).

Saturation intensity

The saturation intensity I_S is defined as the input intensity at which the gain of the optical amplifier drops to exactly half of the small-signal gain. We can compute the saturation intensity as

IS=hνσ(ν)⋅τSdisplaystyle I_S=hnu over sigma (nu )cdot tau _S

where

h is Planck's constant, and

τ_S is the saturation time constant, which depends^{[citation needed]} on the spontaneous emission lifetimes of the various transitions between the energy levels related to the amplification.

νdisplaystyle nu is the frequency in Hz

General gain equation

The general form of the gain equation, which applies regardless of the input intensity, derives from the general differential equation for the intensity I as a function of position z in the gain medium:

dIdz=γ0(ν)1+g¯(ν)I(z)IS⋅I(z)displaystyle dI over dz=gamma _0(nu ) over 1+bar g(nu )I(z) over I_Scdot I(z)

where ISdisplaystyle I_S is saturation intensity. To solve, we first rearrange the equation in order to separate the variables, intensity I and position z:

dII(z)[1+g¯(ν)I(z)IS]=γ0(ν)⋅dzdisplaystyle dI over I(z)left[1+bar g(nu )I(z) over I_Sright]=gamma _0(nu )cdot dz

Integrating both sides, we obtain

ln⁡(I(z)Iin)+g¯(ν)I(z)−IinIS=γ0(ν)⋅zdisplaystyle ln left(I(z) over I_inright)+bar g(nu )I(z)-I_in over I_S=gamma _0(nu )cdot z

or

ln⁡(I(z)Iin)+g¯(ν)IinIS(I(z)Iin−1)=γ0(ν)⋅zdisplaystyle ln left(I(z) over I_inright)+bar g(nu )I_in over I_Sleft(I(z) over I_in-1right)=gamma _0(nu )cdot z

The gain G of the amplifier is defined as the optical intensity I at position z divided by the input intensity:

G=G(z)=I(z)Iindisplaystyle G=G(z)=I(z) over I_in

Substituting this definition into the prior equation, we find the general gain equation:

ln⁡(G)+g¯(ν)IinIS(G−1)=γ0(ν)⋅zdisplaystyle ln left(Gright)+bar g(nu )I_in over I_Sleft(G-1right)=gamma _0(nu )cdot z

Small signal approximation

In the special case where the input signal is small compared to the saturation intensity, in other words,

Iin≪ISdisplaystyle I_inll I_S,

then the general gain equation gives the small signal gain as

ln⁡(G)=ln⁡(G0)=γ0(ν)⋅zdisplaystyle ln(G)=ln(G_0)=gamma _0(nu )cdot z

or

G=G0=eγ0(ν)zdisplaystyle G=G_0=e^gamma _0(nu )z

which is identical to the small signal gain equation (see above).

Large signal asymptotic behavior

For large input signals, where

Iin≫ISdisplaystyle I_ingg I_S,

the gain approaches unity

G→1displaystyle Grightarrow 1

and the general gain equation approaches a linear asymptote:

I(z)=Iin+γ0(ν)⋅zg¯(ν)ISdisplaystyle I(z)=I_in+gamma _0(nu )cdot z over bar g(nu )I_S

See also

References

• 
  Saleh, Bahaa E. A. & Teich, Malvin Carl (1991). Fundamentals of Photonics. New York: John Wiley & Sons. ISBN 0-471-83965-5.
  


• 
  Alan Corney (1977). Atomic and Laser Spectroscopy. Oxford: Oxford Uni. Press. ISBN 0-19-921145-0.
  
  ISBN 978-0-19-921145-6.

.3 Laser Fundamentals, William T. Silfvast