Snub 24-cell honeycomb
| Snub 24-cell honeycomb | |
|---|---|
| (No image) | |
| Type | Uniform 4-honeycomb |
| Schläfli symbols | s3,4,3,3 sr3,3,4,3 2sr4,3,3,4 2sr4,3,31,1 s31,1,1,1 |
| Coxeter diagrams |
|
| 4-face type | snub 24-cell 16-cell 5-cell |
| Cell type | 3,3 3,5 |
| Face type | triangle 3 |
| Vertex figure | 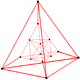 Irregular decachoron |
| Symmetries | [3+,4,3,3] [3,4,(3,3)+] [4,(3,3)+,4] [4,(3,31,1)+] [31,1,1,1]+ |
| Properties | Vertex transitive, nonWythoffian |
In four-dimensional Euclidean geometry, the snub 24-cell honeycomb, or snub icositetrachoric honeycomb is a uniform space-filling tessellation (or honeycomb) by snub 24-cells, 16-cells, and 5-cells. It was discovered by Thorold Gosset with his 1900 paper of semiregular polytopes. It is not semiregular by Gosset's definition of regular facets, but all of its cells (ridges) are regular, either tetrahedra or icosahedra.
It can be seen as an alternation of a truncated 24-cell honeycomb, and can be represented by Schläfli symbol s3,4,3,3, s31,1,1,1, and 3 other snub constructions.
It is defined by an irregular decachoron vertex figure (10-celled 4-polytope), faceted by four snub 24-cells, one 16-cell, and five 5-cells. The vertex figure can be seen topologically as a modified tetrahedral prism, where one of the tetrahedra is subdivided at mid-edges into a central octahedron and four corner tetrahedra. Then the four side-facets of the prism, the triangular prisms become tridiminished icosahedra.
Symmetry constructions
There are five different symmetry constructions of this tessellation. Each symmetry can be represented by different arrangements of colored snub 24-cell, 16-cell, and 5-cell facets. In all cases, four snub 24-cells, five 5-cells, and one 16-cell meet at each vertex, but the vertex figures have different symmetry generators.
Symmetry | Coxeter Schläfli | Facets (on vertex figure) | ||
|---|---|---|---|---|
Snub 24-cell (4) | 16-cell (1) | 5-cell (5) | ||
| [3+,4,3,3] | s3,4,3,3 | 4: | ||
| [3,4,(3,3)+] | sr3,3,4,3 | 3: 1: | ||
| [[4,(3,3)+,4]] | 2sr4,3,3,4 | 2,2: | ||
| [(31,1,3)+,4] | 2sr4,3,31,1 | 1,1: 2: | ||
| [31,1,1,1]+ | s31,1,1,1 | 1,1,1,1: | ||
See also
Regular and uniform honeycombs in 4-space:
- Tesseractic honeycomb
- 16-cell honeycomb
- 24-cell honeycomb
- Truncated 24-cell honeycomb
- 5-cell honeycomb
- Truncated 5-cell honeycomb
- Omnitruncated 5-cell honeycomb
References
T. Gosset: On the Regular and Semi-Regular Figures in Space of n Dimensions, Messenger of Mathematics, Macmillan, 1900
Coxeter, H.S.M. Regular Polytopes, (3rd edition, 1973), Dover edition, .mw-parser-output cite.citationfont-style:inherit.mw-parser-output qquotes:"""""""'""'".mw-parser-output code.cs1-codecolor:inherit;background:inherit;border:inherit;padding:inherit.mw-parser-output .cs1-lock-free abackground:url("//upload.wikimedia.org/wikipedia/commons/thumb/6/65/Lock-green.svg/9px-Lock-green.svg.png")no-repeat;background-position:right .1em center.mw-parser-output .cs1-lock-limited a,.mw-parser-output .cs1-lock-registration abackground:url("//upload.wikimedia.org/wikipedia/commons/thumb/d/d6/Lock-gray-alt-2.svg/9px-Lock-gray-alt-2.svg.png")no-repeat;background-position:right .1em center.mw-parser-output .cs1-lock-subscription abackground:url("//upload.wikimedia.org/wikipedia/commons/thumb/a/aa/Lock-red-alt-2.svg/9px-Lock-red-alt-2.svg.png")no-repeat;background-position:right .1em center.mw-parser-output .cs1-subscription,.mw-parser-output .cs1-registrationcolor:#555.mw-parser-output .cs1-subscription span,.mw-parser-output .cs1-registration spanborder-bottom:1px dotted;cursor:help.mw-parser-output .cs1-hidden-errordisplay:none;font-size:100%.mw-parser-output .cs1-visible-errorfont-size:100%.mw-parser-output .cs1-subscription,.mw-parser-output .cs1-registration,.mw-parser-output .cs1-formatfont-size:95%.mw-parser-output .cs1-kern-left,.mw-parser-output .cs1-kern-wl-leftpadding-left:0.2em.mw-parser-output .cs1-kern-right,.mw-parser-output .cs1-kern-wl-rightpadding-right:0.2em
ISBN 0-486-61480-8 p. 296, Table II: Regular honeycombs
Kaleidoscopes: Selected Writings of H.S.M. Coxeter, edited by F. Arthur Sherk, Peter McMullen, Anthony C. Thompson, Asia Ivic Weiss, Wiley-Interscience Publication, 1995,
ISBN 978-0-471-01003-6- (Paper 24) H.S.M. Coxeter, Regular and Semi-Regular Polytopes III, [Math. Zeit. 200 (1988) 3-45]
- George Olshevsky, Uniform Panoploid Tetracombs, Manuscript (2006) (Complete list of 11 convex uniform tilings, 28 convex uniform honeycombs, and 143 convex uniform tetracombs) Model 133
Klitzing, Richard. "4D Euclidean tesselations"., o4s3s3s4o, s3s3s *b3s4o, s3s3s *b3s *b3s, o3o3o4s3s, s3s3s4o3o - sadit - O133
Fundamental convex regular and uniform honeycombs in dimensions 2-9 | ||||||
|---|---|---|---|---|---|---|
| Space | Family | A~n−1displaystyle tilde A_n-1  | C~n−1displaystyle tilde C_n-1  | B~n−1displaystyle tilde B_n-1  | D~n−1displaystyle tilde D_n-1  | G~2displaystyle tilde G_2  / F~4displaystyle tilde F_4 / F~4displaystyle tilde F_4 / E~n−1displaystyle tilde E_n-1 / E~n−1displaystyle tilde E_n-1 |
| E2 | Uniform tiling | 3[3] | δ3 | hδ3 | qδ3 | Hexagonal |
| E3 | Uniform convex honeycomb | 3[4] | δ4 | hδ4 | qδ4 | |
| E4 | Uniform 4-honeycomb | 3[5] | δ5 | hδ5 | qδ5 | 24-cell honeycomb |
| E5 | Uniform 5-honeycomb | 3[6] | δ6 | hδ6 | qδ6 | |
| E6 | Uniform 6-honeycomb | 3[7] | δ7 | hδ7 | qδ7 | 222 |
| E7 | Uniform 7-honeycomb | 3[8] | δ8 | hδ8 | qδ8 | 133 • 331 |
| E8 | Uniform 8-honeycomb | 3[9] | δ9 | hδ9 | qδ9 | 152 • 251 • 521 |
| E9 | Uniform 9-honeycomb | 3[10] | δ10 | hδ10 | qδ10 | |
| En-1 | Uniform (n-1)-honeycomb | 3[n] | δn | hδn | qδn | 1k2 • 2k1 • k21 |