16-cell honeycomb
| 16-cell honeycomb | |
|---|---|
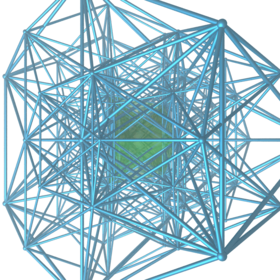 Perspective projection: the first layer of adjacent 16-cell facets. | |
| Type | Regular 4-honeycomb Uniform 4-honeycomb |
| Family | Alternated hypercube honeycomb |
| Schläfli symbol | 3,3,4,3 |
| Coxeter diagrams |       =    =    |
| 4-face type | 3,3,4  |
| Cell type | 3,3  |
| Face type | 3 |
| Edge figure | cube |
| Vertex figure |  24-cell |
| Coxeter group | F~4displaystyle tilde F_4  = [3,3,4,3] |
| Dual | 3,4,3,3 |
| Properties | vertex-transitive, edge-transitive, face-transitive, cell-transitive, 4-face-transitive |
In four-dimensional Euclidean geometry, the 16-cell honeycomb is one of the three regular space-filling tessellations (or honeycombs) in Euclidean 4-space. The other two are its dual the 24-cell honeycomb, and the tesseractic honeycomb. This honeycomb is constructed from 16-cell facets, three around every face. It has a 24-cell vertex figure.
This vertex arrangement or lattice is called the B4, D4, or F4 lattice.[1][2]
Contents
1 Alternate names
2 Coordinates
3 D4 lattice
4 Symmetry constructions
5 Related honeycombs
6 See also
7 Notes
8 References
Alternate names
- Hexadecachoric tetracomb/honeycomb
- Demitesseractic tetracomb/honeycomb
Coordinates
As a regular honeycomb, 3,3,4,3, it has a 2-dimensional analogue, 3,6, and as an alternated form (the demitesseractic honeycomb, h4,3,3,4) it is related to the alternated cubic honeycomb.
Vertices can be placed at all integer coordinates (i,j,k,l), such that the sum of the coordinates is even.
D4 lattice
The vertex arrangement of the 16-cell honeycomb is called the D4 lattice or F4 lattice.[2] The vertices of this lattice are the centers of the 3-spheres in the densest known packing of equal spheres in 4-space;[3] its kissing number is 24, which is also the same as the kissing number in R4, as proved by Oleg Musin in 2003.[4][5]
The D+
4 lattice (also called D2
4) can be constructed by the union of two D4 lattices, and is identical to the tesseractic honeycomb:[6]
∪ 
= 
=
This packing is only a lattice for even dimensions. The kissing number is 23 = 8, (2n – 1 for n < 8, 240 for n = 8, and 2n(n – 1) for n > 8).[7]
The D*
4 lattice (also called D4
4 and C2
4) can be constructed by the union of all four D4 lattices, but it is identical to the D4 lattice: It is also the 4-dimensional body centered cubic, the union of two 4-cube honeycombs in dual positions.[8]
- ∪ ∪
∪ 
= = 
∪ 
.
The kissing number of the D*
4 lattice (and D4 lattice) is 24[9] and its Voronoi tessellation is a 24-cell honeycomb, , containing all rectified 16-cells (24-cell) Voronoi cells, or .[10]
Symmetry constructions
There are three different symmetry constructions of this tessellation. Each symmetry can be represented by different arrangements of colored 16-cell facets.
Coxeter group | Schläfli symbol | Coxeter diagram | Vertex figure Symmetry | Facets/verf |
|---|---|---|---|---|
F~4displaystyle tilde F_4 = [3,3,4,3] | 3,3,4,3 | | [3,4,3], order 1152 | 24: 16-cell |
B~4displaystyle tilde B_4  = [31,1,3,4] | = h4,3,3,4 | = | [3,3,4], order 384 | 16+8: 16-cell |
D~4displaystyle tilde D_4  = [31,1,1,1] | 3,31,1,1 = h4,3,31,1 | = | [31,1,1], order 192 | 8+8+8: 16-cell |
2×½C~4displaystyle tilde C_4 = [[(4,3,3,4,2+)]] | ht0,44,3,3,4 | | 8+4+4: 4-demicube 8: 16-cell |
Related honeycombs
It is related to the regular hyperbolic 5-space 5-orthoplex honeycomb, 3,3,3,4,3, with 5-orthoplex facets, the regular 4-polytope 24-cell, 3,4,3 with octahedral (3-orthoplex) cell, and cube 4,3, with (2-orthoplex) square faces.
This honeycomb is one of 20 uniform honeycombs constructed by the D~5displaystyle tilde D_5
| D5 honeycombs | |||
|---|---|---|---|
Extended symmetry | Extended diagram | Extended group | Honeycombs |
| [31,1,3,31,1] | | D~5displaystyle tilde D_5 |  |
| <[31,1,3,31,1]> ↔ [31,1,3,3,4] |     ↔  | D~5displaystyle tilde D_5 ×21 = B~5displaystyle tilde B_5 |  , , ,
|
| [[31,1,3,31,1]] | | D~5displaystyle tilde D_5 ×22 | , |
| <2[31,1,3,31,1]> ↔ [4,3,3,3,4] |    ↔  | D~5displaystyle tilde D_5 ×41 = C~5displaystyle tilde C_5 | , , , , , |
| [<2[31,1,3,31,1]>] ↔ [[4,3,3,3,4]] | ↔ | D~5displaystyle tilde D_5 ×8 = C~5displaystyle tilde C_5×2 | , , |
See also
Regular and uniform honeycombs in 4-space:
- Tesseractic honeycomb
- 24-cell honeycomb
- Truncated 24-cell honeycomb
- Snub 24-cell honeycomb
- 5-cell honeycomb
- Truncated 5-cell honeycomb
- Omnitruncated 5-cell honeycomb
Notes
^ http://www.math.rwth-aachen.de/~Gabriele.Nebe/LATTICES/F4.html
^ ab http://www.math.rwth-aachen.de/~Gabriele.Nebe/LATTICES/D4.html
^ Conway and Sloane, Sphere packings, lattices, and groups, 1.4 n-dimensional packings, p.9
^ Conway and Sloane, Sphere packings, lattices, and groups, 1.5 Sphere packing problem summary of results. , p.12
^ O. R. Musin (2003). "The problem of the twenty-five spheres". Russ. Math. Surv. 58: 794–795. Bibcode:2003RuMaS..58..794M. doi:10.1070/RM2003v058n04ABEH000651..mw-parser-output cite.citationfont-style:inherit.mw-parser-output qquotes:"""""""'""'".mw-parser-output code.cs1-codecolor:inherit;background:inherit;border:inherit;padding:inherit.mw-parser-output .cs1-lock-free abackground:url("//upload.wikimedia.org/wikipedia/commons/thumb/6/65/Lock-green.svg/9px-Lock-green.svg.png")no-repeat;background-position:right .1em center.mw-parser-output .cs1-lock-limited a,.mw-parser-output .cs1-lock-registration abackground:url("//upload.wikimedia.org/wikipedia/commons/thumb/d/d6/Lock-gray-alt-2.svg/9px-Lock-gray-alt-2.svg.png")no-repeat;background-position:right .1em center.mw-parser-output .cs1-lock-subscription abackground:url("//upload.wikimedia.org/wikipedia/commons/thumb/a/aa/Lock-red-alt-2.svg/9px-Lock-red-alt-2.svg.png")no-repeat;background-position:right .1em center.mw-parser-output .cs1-subscription,.mw-parser-output .cs1-registrationcolor:#555.mw-parser-output .cs1-subscription span,.mw-parser-output .cs1-registration spanborder-bottom:1px dotted;cursor:help.mw-parser-output .cs1-hidden-errordisplay:none;font-size:100%.mw-parser-output .cs1-visible-errorfont-size:100%.mw-parser-output .cs1-subscription,.mw-parser-output .cs1-registration,.mw-parser-output .cs1-formatfont-size:95%.mw-parser-output .cs1-kern-left,.mw-parser-output .cs1-kern-wl-leftpadding-left:0.2em.mw-parser-output .cs1-kern-right,.mw-parser-output .cs1-kern-wl-rightpadding-right:0.2em
^ Conway and Sloane, Sphere packings, lattices, and groups, 7.3 The packing D3+, p.119
^ Conway and Sloane, Sphere packings, lattices, and groups, p. 119
^ Conway and Sloane, Sphere packings, lattices, and groups, 7.4 The dual lattice D3*, p.120
^ Conway and Sloane, Sphere packings, lattices, and groups, p. 120
^ Conway and Sloane, Sphere packings, lattices, and groups, p. 466
References
Coxeter, H.S.M. Regular Polytopes, (3rd edition, 1973), Dover edition,
ISBN 0-486-61480-8- pp. 154–156: Partial truncation or alternation, represented by h prefix: h4,4 = 4,4; h4,3,4 = 31,1,4, h4,3,3,4 = 3,3,4,3, ...
Kaleidoscopes: Selected Writings of H.S.M. Coxeter, edited by F. Arthur Sherk, Peter McMullen, Anthony C. Thompson, Asia Ivic Weiss, Wiley-Interscience Publication, 1995,
ISBN 978-0-471-01003-6 [1]- (Paper 24) H.S.M. Coxeter, Regular and Semi-Regular Polytopes III, [Math. Zeit. 200 (1988) 3-45]
- George Olshevsky, Uniform Panoploid Tetracombs, Manuscript (2006) (Complete list of 11 convex uniform tilings, 28 convex uniform honeycombs, and 143 convex uniform tetracombs)
Klitzing, Richard. "4D Euclidean tesselations". x3o3o4o3o - hext - O104
Conway JH, Sloane NJH (1998). Sphere Packings, Lattices and Groups (3rd ed.). ISBN 0-387-98585-9.
Fundamental convex regular and uniform honeycombs in dimensions 2-9 | ||||||
|---|---|---|---|---|---|---|
| Space | Family | A~n−1displaystyle tilde A_n-1  | C~n−1displaystyle tilde C_n-1  | B~n−1displaystyle tilde B_n-1  | D~n−1displaystyle tilde D_n-1  | G~2displaystyle tilde G_2  / F~4displaystyle tilde F_4 / E~n−1displaystyle tilde E_n-1 |
| E2 | Uniform tiling | 3[3] | δ3 | hδ3 | qδ3 | Hexagonal |
| E3 | Uniform convex honeycomb | 3[4] | δ4 | hδ4 | qδ4 | |
| E4 | Uniform 4-honeycomb | 3[5] | δ5 | hδ5 | qδ5 | 24-cell honeycomb |
| E5 | Uniform 5-honeycomb | 3[6] | δ6 | hδ6 | qδ6 | |
| E6 | Uniform 6-honeycomb | 3[7] | δ7 | hδ7 | qδ7 | 222 |
| E7 | Uniform 7-honeycomb | 3[8] | δ8 | hδ8 | qδ8 | 133 • 331 |
| E8 | Uniform 8-honeycomb | 3[9] | δ9 | hδ9 | qδ9 | 152 • 251 • 521 |
| E9 | Uniform 9-honeycomb | 3[10] | δ10 | hδ10 | qδ10 | |
| En-1 | Uniform (n-1)-honeycomb | 3[n] | δn | hδn | qδn | 1k2 • 2k1 • k21 |
