Dfyjkt

A Lévy flight, named for French mathematician Paul Lévy, is a random walk in which the step-lengths have a probability distribution that is heavy-tailed. When defined as a walk in a space of dimension greater than one, the steps made are in isotropic random directions.

The term "Lévy flight" was coined by Benoît Mandelbrot,^[1] who used this for one specific definition of the distribution of step sizes. He used the term Cauchy flight for the case where the distribution of step sizes is a Cauchy distribution,^[2] and Rayleigh flight for when the distribution is a normal distribution^[3] (which is not an example of a heavy-tailed probability distribution).

Later researchers have extended the use of the term "Lévy flight" to include cases where the random walk takes place on a discrete grid rather than on a continuous space.^[4][5]

The particular case for which Mandelbrot used the term "Lévy flight"^[1] is defined by the survivor function (commonly known as the survival function) of the distribution of step-sizes, U, being^[6]

Pr(U>u)={1: u<1,u−D: u≥1.displaystyle Pr(U>u)=begincases1&: u<1,\u^-D&: ugeq 1.endcases

Here D is a parameter related to the fractal dimension and the distribution is a particular case of the Pareto distribution. Later researchers allow the distribution of step sizes to be any distribution for which the survival function has a power-like tail^{[citation needed]}

Pr(U>u)=O(u−k),displaystyle Pr(U>u)=O(u^-k),

for some k satisfying 1 < k < 3. (Here the notation O is the Big O notation.) Such distributions have an infinite variance. Typical examples are the symmetric stable distributions.

Properties

Lévy flights are, by construction, Markov processes. For general distributions of the step-size, satisfying the power-like condition, the distance from the origin of the random walk tends, after a large number of steps, to a stable distribution due to the generalized central limit theorem, enabling many processes to be modeled using Lévy flights.

The probability densities for particles undergoing a Levy flight can be modeled using a generalized version of the Fokker–Planck equation, which is usually used to model Brownian motion. The equation requires the use of fractional derivatives. For jump lengths which have a symmetric probability distribution, the equation takes a simple form in terms of the Riesz fractional derivative. In one dimension, the equation reads as

∂φ(x,t)∂t=−∂∂xf(x,t)φ(x,t)+γ∂αφ(x,t)∂|x|αdisplaystyle frac partial varphi (x,t)partial t=-frac partial partial xf(x,t)varphi (x,t)+gamma frac partial ^alpha varphi (x,t)partial

where γ is a constant akin to the diffusion constant, α is the stability parameter and f(x,t) is the potential. The Riesz derivative can be understood in terms of its Fourier Transform.

Fk[∂αφ(x,t)∂|x|α]=kαFk[φ(x,t)]displaystyle F_kleft[frac partial ^alpha varphi (x,t)partial right]=k^alpha F_k[varphi (x,t)]

This can be easily extended to multiple dimensions.

Another important property of the Lévy is that of diverging variances in all cases except that of α = 2, i.e. Brownian motion. In general, the θ fractional moment of the distribution diverges if α < θ. Also,

⟨|x|θ⟩∝tθ/α if θ≤α.displaystyle langle

The exponential scaling of the step lengths gives Lévy flights a scale invariant property,^{[citation needed]} and they are used to model data that exhibits clustering.^{[citation needed]}

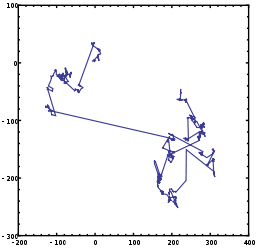
Figure 1. An example of 1000 steps of a Lévy flight in two dimensions. The origin of the motion is at [0,0], the angular direction is uniformly distributed and the step size is distributed according to a Lévy (i.e. stable) distribution with α = 1 and β = 0 which is a Cauchy distribution. Note the presence of large jumps in location compared to the Brownian motion illustrated in Figure 2.

Figure 2. An example of 1000 steps of an approximation to a Brownian motion type of Lévy flight in two dimensions. The origin of the motion is at [0, 0], the angular direction is uniformly distributed and the step size is distributed according to a Lévy (i.e. stable) distribution with α = 2 and β = 0 (i.e., a normal distribution).

Applications

The definition of a Lévy flight stems from the mathematics related to chaos theory and is useful in stochastic measurement and simulations for random or pseudo-random natural phenomena. Examples include earthquake data analysis, financial mathematics, cryptography, signals analysis as well as many applications in astronomy, biology, and physics.

Another application is the Lévy flight foraging hypothesis. When sharks and other ocean predators can’t find food, they abandon Brownian motion, the random motion seen in swirling gas molecules, for Lévy flight — a mix of long trajectories and short, random movements found in turbulent fluids. Researchers analyzed over 12 million movements recorded over 5,700 days in 55 data-logger-tagged animals from 14 ocean predator species in the Atlantic and Pacific Oceans, including silky sharks, yellowfin tuna, blue marlin and swordfish. The data showed that Lévy flights interspersed with Brownian motion can describe the animals' hunting patterns.^{[7][8][9][10]} Birds and other animals^[11] (including humans)^[12] follow paths that have been modeled using Lévy flight (e.g. when searching for food).^[13] Biological flight data can also apparently be mimicked by other models such as composite correlated random walks, which grow across scales to converge on optimal Lévy walks.^[14] Composite Brownian walks can be finely tuned to theoretically optimal Lévy walks but they are not as efficient as Lévy search across most landscapes types, suggesting selection pressure for Lévy walk characteristics is more likely than multi-scaled normal diffusive patterns.^[15]

Efficient routing in a network can be performed by links having a Levy flight length distribution with specific values of alpha.^[4][5]

See also

• Fat-tailed distribution


• Heavy-tailed distribution


• Lévy process


• Lévy alpha-stable distribution


• Lévy flight foraging hypothesis

Notes

References

• 
  Mandelbrot, Benoit B. (1982). The Fractal Geometry of Nature (Updated and augm. ed.). New York: W. H. Freeman. ISBN 0-7167-1186-9. OCLC 7876824.
  

Further reading

• 
  Viswanathan, G.; Bartumeus, F.; v. Buldyrev, S.; Catalan, J.; Fulco, U.; Havlin, S.; Da Luz, M.; Lyra, M.; Raposo, E.; Eugene Stanley, H. (2002). "Lévy flight random searches in biological phenomena". Physica A: Statistical Mechanics and its Applications. 314: 208–213. Bibcode:2002PhyA..314..208V. doi:10.1016/S0378-4371(02)01157-3.
  


• 
  Viswanathan, G.; Afanasyev, V.; Buldyrev, S.; Havlin, S.; Daluz, M.; Raposo, E.; Stanley, H. (2000). "Lévy flights in random searches". Physica A: Statistical Mechanics and its Applications. 282: 1–12. Bibcode:2000PhyA..282....1V. doi:10.1016/S0378-4371(00)00071-6.
  


• 
  Cheng, Z.; Savit, R. (1987). "Fractal and nonfractal behavior in Levy flights" (PDF). Journal of Mathematical Physics. 28 (3): 592. Bibcode:1987JMP....28..592C. doi:10.1063/1.527644.
  


• 
  Shlesinger, Michael F.; Klafter, Joseph; Zumofen, Gert (December 1999). "Above, below and beyond Brownian motion" (PDF). American Journal of Physics. 67 (12): 1253–1259. Bibcode:1999AmJPh..67.1253S. doi:10.1119/1.19112. Archived from the original (PDF) on 2012-03-28.
  

External links

• A comparison of the paintings of Jackson Pollock to a Lévy flight model