Dfyjkt

There are several kinds of means in various branches of mathematics (especially statistics).

For a data set, the arithmetic mean, also called the mathematical expectation or average, is the central value of a discrete set of numbers: specifically, the sum of the values divided by the number of values. The arithmetic mean of a set of numbers x₁, x₂, ..., x_n is typically denoted by x¯displaystyle bar x, pronounced "x bar". If the data set were based on a series of observations obtained by sampling from a statistical population, the arithmetic mean is the sample mean (denoted x¯displaystyle bar x) to distinguish it from the mean of the underlying distribution, the population mean (denoted μdisplaystyle mu or μxdisplaystyle mu _x).^[1] Pronounced "mew" /'mjuː/.

In probability and statistics, the population mean, or expected value, are a measure of the central tendency either of a probability distribution or of the random variable characterized by that distribution.^[2] In the case of a discrete probability distribution of a random variable X, the mean is equal to the sum over every possible value weighted by the probability of that value; that is, it is computed by taking the product of each possible value x of X and its probability p(x), and then adding all these products together, giving μ=∑xp(x)displaystyle mu =sum xp(x).^[3] An analogous formula applies to the case of a continuous probability distribution. Not every probability distribution has a defined mean; see the Cauchy distribution for an example. Moreover, for some distributions the mean is infinite.

For a finite population, the population mean of a property is equal to the arithmetic mean of the given property while considering every member of the population. For example, the population mean height is equal to the sum of the heights of every individual divided by the total number of individuals. The sample mean may differ from the population mean, especially for small samples. The law of large numbers dictates that the larger the size of the sample, the more likely it is that the sample mean will be close to the population mean.^[4]

Outside probability and statistics, a wide range of other notions of "mean" are often used in geometry and analysis; examples are given below.

Types of mean

Pythagorean means

Arithmetic mean (AM)

The arithmetic mean (or simply mean) of a sample x1,x2,…,xndisplaystyle x_1,x_2,ldots ,x_n, usually denoted by x¯displaystyle bar x, is the sum of the sampled values divided by the number of items in the example

x¯=1n(∑i=1nxi)=x1+x2+⋯+xnndisplaystyle bar x=frac 1nleft(sum _i=1^nx_iright)=frac x_1+x_2+cdots +x_nn

For example, the arithmetic mean of five values: 4, 36, 45, 50, 75 is:

4+36+45+50+755=2105=42.displaystyle frac 4+36+45+50+755=frac 2105=42.

Geometric mean (GM)

The geometric mean is an average that is useful for sets of positive numbers that are interpreted according to their product and not their sum (as is the case with the arithmetic mean); e.g., rates of growth.

x¯=(∏i=1nxi)1n=(x1x2⋯xn)1ndisplaystyle bar x=left(prod _i=1^nx_iright)^frac 1n=left(x_1x_2cdots x_nright)^frac 1n

For example, the geometric mean of five values: 4, 36, 45, 50, 75 is:

(4×36×45×50×75)15=243000005=30.displaystyle (4times 36times 45times 50times 75)^frac 15=sqrt[5]24;300;000=30.

Harmonic mean (HM)

The harmonic mean is an average which is useful for sets of numbers which are defined in relation to some unit, for example speed (distance per unit of time).

x¯=n(∑i=1n1xi)−1displaystyle bar x=nleft(sum _i=1^nfrac 1x_iright)^-1

For example, the harmonic mean of the five values: 4, 36, 45, 50, 75 is

514+136+145+150+175=513=15.displaystyle frac 5tfrac 14+tfrac 136+tfrac 145+tfrac 150+tfrac 175=frac 5;tfrac 13;=15.

Relationship between AM, GM, and HM

AM, GM, and HM satisfy these inequalities:

AM≥GM≥HMdisplaystyle mathrm AM geq mathrm GM geq mathrm HM ,

Equality holds if and only if all the elements of the given sample are equal.

Statistical location

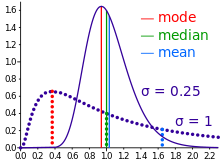
Comparison of the arithmetic mean, median and mode of two skewed (log-normal) distributions.

Geometric visualization of the mode, median and mean of an arbitrary probability density function.^[5]

In descriptive statistics, the mean may be confused with the median, mode or mid-range, as any of these may be called an "average" (more formally, a measure of central tendency). The mean of a set of observations is the arithmetic average of the values; however, for skewed distributions, the mean is not necessarily the same as the middle value (median), or the most likely value (mode). For example, mean income is typically skewed upwards by a small number of people with very large incomes, so that the majority have an income lower than the mean. By contrast, the median income is the level at which half the population is below and half is above. The mode income is the most likely income and favors the larger number of people with lower incomes. While the median and mode are often more intuitive measures for such skewed data, many skewed distributions are in fact best described by their mean, including the exponential and Poisson distributions.

Mean of a probability distribution

The mean of a probability distribution is the long-run arithmetic average value of a random variable having that distribution. In this context, it is also known as the expected value. For a discrete probability distribution, the mean is given by ∑xP(x)displaystyle textstyle sum xP(x), where the sum is taken over all possible values of the random variable and P(x)displaystyle P(x) is the probability mass function. For a continuous distribution,the mean is ∫−∞∞xf(x)dxdisplaystyle textstyle int _-infty ^infty xf(x),dx, where f(x)displaystyle f(x) is the probability density function. In all cases, including those in which the distribution is neither discrete nor continuous, the mean is the Lebesgue integral of the random variable with respect to its probability measure. The mean need not exist or be finite; for some probability distributions the mean is infinite (+∞ or −∞), while others have no mean.

Generalized means

Power mean

The generalized mean, also known as the power mean or Hölder mean, is an abstraction of the quadratic, arithmetic, geometric and harmonic means. It is defined for a set of n positive numbers x_i by

x¯(m)=(1n∑i=1nxim)1mdisplaystyle bar x(m)=left(frac 1nsum _i=1^nx_i^mright)^frac 1m

By choosing different values for the parameter m, the following types of means are obtained:

m→∞displaystyle mrightarrow infty	maximum of xidisplaystyle x_i
m=2displaystyle m=2	quadratic mean
m=1displaystyle m=1	arithmetic mean
m→0displaystyle mrightarrow 0	geometric mean
m=−1displaystyle m=-1	harmonic mean
m→−∞displaystyle mrightarrow -infty	minimum of xidisplaystyle x_i

ƒ-mean

This can be generalized further as the generalized ƒ-mean

x¯=f−1(1n∑i=1nf(xi))displaystyle bar x=f^-1left(frac 1nsum _i=1^nfleft(x_iright)right)

and again a suitable choice of an invertible ƒ will give

f(x)=xdisplaystyle f(x)=x	arithmetic mean,
f(x)=1xdisplaystyle f(x)=frac 1x	harmonic mean,
f(x)=xmdisplaystyle f(x)=x^m	power mean,
f(x)=ln⁡(x)displaystyle f(x)=ln(x)	geometric mean.

Weighted arithmetic mean

The weighted arithmetic mean (or weighted average) is used if one wants to combine average values from samples of the same population with different sample sizes:

x¯=∑i=1nwixi∑i=1nwi.displaystyle bar x=frac sum _i=1^nw_ix_isum _i=1^nw_i.

The weights widisplaystyle w_i represent the sizes of the different samples. In other applications, they represent a measure for the reliability of the influence upon the mean by the respective values.

Truncated mean

Sometimes a set of numbers might contain outliers, i.e., data values which are much lower or much higher than the others.
Often, outliers are erroneous data caused by artifacts. In this case, one can use a truncated mean. It involves discarding given parts of the data at the top or the bottom end, typically an equal amount at each end and then taking the arithmetic mean of the remaining data. The number of values removed is indicated as a percentage of the total number of values.

Interquartile mean

The interquartile mean is a specific example of a truncated mean. It is simply the arithmetic mean after removing the lowest and the highest quarter of values.

x¯=2n∑i=n4+134nxidisplaystyle bar x=frac 2n;sum _i=frac n4+1^frac 34n!!x_i

assuming the values have been ordered, so is simply a specific example of a weighted mean for a specific set of weights.

Mean of a function

In some circumstances mathematicians may calculate a mean of an infinite (even an uncountable) set of values. This can happen when calculating the mean value yavedisplaystyle y_textave of a function f(x)displaystyle f(x). Intuitively this can be thought of as calculating the area under a section of a curve and then dividing by the length of that section. This can be done crudely by counting squares on graph paper or more precisely by integration. The integration formula is written as:

yave(a,b)=1b−a∫abf(x)dxdisplaystyle y_textave(a,b)=frac 1b-aint limits _a^b!f(x),dx

Care must be taken to make sure that the integral converges. But the mean may be finite even if the function itself tends to infinity at some points.

Mean of angles and cyclical quantities

Angles, times of day, and other cyclical quantities require modular arithmetic to add and otherwise combine numbers. In all these situations, there will not be a unique mean. For example, the times an hour before and after midnight are equidistant to both midnight and noon. It is also possible that no mean exists. Consider a color wheel -- there is no mean to the set of all colors. In these situations, you must decide which mean is most useful. You can do this by adjusting the values before averaging, or by using a specialized approach for the mean of circular quantities.

Fréchet mean

The Fréchet mean gives a manner for determining the "center" of a mass distribution on a surface or, more generally, Riemannian manifold. Unlike many other means, the Fréchet mean is defined on a space whose elements cannot necessarily be added together or multiplied by scalars.
It is sometimes also known as the Karcher mean (named after Hermann Karcher).

Other means

Distribution of the sample mean

The arithmetic mean of a population, or population mean, is often denoted μ. The sample mean x¯displaystyle bar x (the arithmetic mean of a sample of values drawn from the population) makes a good estimator of the population mean, as its expected value is equal to the population mean (that is, it is an unbiased estimator). The sample mean is a random variable, not a constant, since its calculated value will randomly differ depending on which members of the population are sampled, and consequently it will have its own distribution. For a random sample of n independent observations, the expected value of the sample mean is

E⁡x¯=μdisplaystyle operatorname E bar x=mu

and the variance of the sample mean is

var⁡(x¯)=σ2n.displaystyle operatorname var (bar x)=frac sigma ^2n.

If the population is normally distributed, then the sample mean is normally distributed:

x¯∼Nμ,σ2n.displaystyle bar xthicksim Nleftmu ,frac sigma ^2nright.

If the population is not normally distributed, the sample mean is nonetheless approximately normally distributed if n is large and σ²/n < +∞. This follows from the central limit theorem.

See also

• Average


• 
  Central tendency
  
  • Median
  
  
  • Mode
  
  


• Descriptive statistics


• Kurtosis


• Law of averages


• Mean value theorem


• Median


• Mode (statistics)


• Summary statistics


• Taylor's law

References