Calculate all possible keys for AES 128 encryption to exploit hardware encryption
$begingroup$
Some background: I am using the MicroChip ATAES132a for hardware encryption/decryption. The ATAES132a is very configurable and can be misconfigured in such a way that the encryption/decryption will be performed using the same nonce. In theory, if the nonce is known I can do an encryption of the plain text and get the same ciphered text result. Based on this, I could possibly try to encrypt the same plain text with the known nonce and compare to the generated ciphered text until I get a match.
For example, in theory my target key could be some thing like this (see below). I would need to calculate every possible key, use the known nonce and the same plain text until I get the same ciphered text result.
const uint8_t g_key0 = 0x01, 0x08, 0x0E, 0x91, 0xe2, 0x64, 0x8f, 0x49, 0x0c, 0xe9, 0x80, 0x45, 0x38, 0xb5, 0x85, 0x3f ;
This would exploit how the device was configured incorrectly. The ATAES132a does all its encryption with AES in CCM mode. I can perform the attack either on the ATAES132a or on any PC using any standard AES library.
Is this attack plausible using a modern PC?
encryption aes
edited Aug 28 '18 at 18:27
psmears
1233
asked Aug 27 '18 at 14:41
PhillyNJPhillyNJ
18018
$endgroup$
add a comment |
$begingroup$
Some background: I am using the MicroChip ATAES132a for hardware encryption/decryption. The ATAES132a is very configurable and can be misconfigured in such a way that the encryption/decryption will be performed using the same nonce. In theory, if the nonce is known I can do an encryption of the plain text and get the same ciphered text result. Based on this, I could possibly try to encrypt the same plain text with the known nonce and compare to the generated ciphered text until I get a match.
For example, in theory my target key could be some thing like this (see below). I would need to calculate every possible key, use the known nonce and the same plain text until I get the same ciphered text result.
const uint8_t g_key0 = 0x01, 0x08, 0x0E, 0x91, 0xe2, 0x64, 0x8f, 0x49, 0x0c, 0xe9, 0x80, 0x45, 0x38, 0xb5, 0x85, 0x3f ;
This would exploit how the device was configured incorrectly. The ATAES132a does all its encryption with AES in CCM mode. I can perform the attack either on the ATAES132a or on any PC using any standard AES library.
Is this attack plausible using a modern PC?
encryption aes
edited Aug 28 '18 at 18:27
psmears
1233
asked Aug 27 '18 at 14:41
PhillyNJPhillyNJ
18018
$endgroup$
$begingroup$
"if the nonce is known I can do an encryption of plain text and get the same ciphered text result" If the nonce is known, you can encrypt null bytes and recover the keystream, and every message that used that nonce is now decrypted
$endgroup$
– Richie Frame
Aug 28 '18 at 10:13
$begingroup$
@RichieFrame How do you recover the keystream?
$endgroup$
– PhillyNJ
Aug 28 '18 at 10:28
1
$begingroup$
CCM mode generates a keystream and XORs it with the plaintext. The keystream is based on the key and nonce, if they are fixed, the keystream is always the same. All you need to do is XOR known or chosen plaintext into the matching ciphertext to recover the keystream
$endgroup$
– Richie Frame
Aug 29 '18 at 0:40
add a comment |
$begingroup$
Some background: I am using the MicroChip ATAES132a for hardware encryption/decryption. The ATAES132a is very configurable and can be misconfigured in such a way that the encryption/decryption will be performed using the same nonce. In theory, if the nonce is known I can do an encryption of the plain text and get the same ciphered text result. Based on this, I could possibly try to encrypt the same plain text with the known nonce and compare to the generated ciphered text until I get a match.
For example, in theory my target key could be some thing like this (see below). I would need to calculate every possible key, use the known nonce and the same plain text until I get the same ciphered text result.
const uint8_t g_key0 = 0x01, 0x08, 0x0E, 0x91, 0xe2, 0x64, 0x8f, 0x49, 0x0c, 0xe9, 0x80, 0x45, 0x38, 0xb5, 0x85, 0x3f ;
This would exploit how the device was configured incorrectly. The ATAES132a does all its encryption with AES in CCM mode. I can perform the attack either on the ATAES132a or on any PC using any standard AES library.
Is this attack plausible using a modern PC?
encryption aes
edited Aug 28 '18 at 18:27
psmears
1233
asked Aug 27 '18 at 14:41
PhillyNJPhillyNJ
18018
$endgroup$
Some background: I am using the MicroChip ATAES132a for hardware encryption/decryption. The ATAES132a is very configurable and can be misconfigured in such a way that the encryption/decryption will be performed using the same nonce. In theory, if the nonce is known I can do an encryption of the plain text and get the same ciphered text result. Based on this, I could possibly try to encrypt the same plain text with the known nonce and compare to the generated ciphered text until I get a match.
For example, in theory my target key could be some thing like this (see below). I would need to calculate every possible key, use the known nonce and the same plain text until I get the same ciphered text result.
const uint8_t g_key0 = 0x01, 0x08, 0x0E, 0x91, 0xe2, 0x64, 0x8f, 0x49, 0x0c, 0xe9, 0x80, 0x45, 0x38, 0xb5, 0x85, 0x3f ;
This would exploit how the device was configured incorrectly. The ATAES132a does all its encryption with AES in CCM mode. I can perform the attack either on the ATAES132a or on any PC using any standard AES library.
Is this attack plausible using a modern PC?
encryption aes
encryption aes
edited Aug 28 '18 at 18:27
psmears
1233
asked Aug 27 '18 at 14:41
PhillyNJPhillyNJ
18018
edited Aug 28 '18 at 18:27
psmears
1233
asked Aug 27 '18 at 14:41
PhillyNJPhillyNJ
18018
edited Aug 28 '18 at 18:27
psmears
1233
edited Aug 28 '18 at 18:27
psmears
1233
edited Aug 28 '18 at 18:27
psmears
1233
1233
asked Aug 27 '18 at 14:41
PhillyNJPhillyNJ
18018
asked Aug 27 '18 at 14:41
PhillyNJPhillyNJ
18018
asked Aug 27 '18 at 14:41
PhillyNJPhillyNJ
18018
18018
$begingroup$
"if the nonce is known I can do an encryption of plain text and get the same ciphered text result" If the nonce is known, you can encrypt null bytes and recover the keystream, and every message that used that nonce is now decrypted
$endgroup$
– Richie Frame
Aug 28 '18 at 10:13
$begingroup$
@RichieFrame How do you recover the keystream?
$endgroup$
– PhillyNJ
Aug 28 '18 at 10:28
1
$begingroup$
CCM mode generates a keystream and XORs it with the plaintext. The keystream is based on the key and nonce, if they are fixed, the keystream is always the same. All you need to do is XOR known or chosen plaintext into the matching ciphertext to recover the keystream
$endgroup$
– Richie Frame
Aug 29 '18 at 0:40
add a comment |
$begingroup$
"if the nonce is known I can do an encryption of plain text and get the same ciphered text result" If the nonce is known, you can encrypt null bytes and recover the keystream, and every message that used that nonce is now decrypted
$endgroup$
– Richie Frame
Aug 28 '18 at 10:13
$begingroup$
@RichieFrame How do you recover the keystream?
$endgroup$
– PhillyNJ
Aug 28 '18 at 10:28
1
$begingroup$
CCM mode generates a keystream and XORs it with the plaintext. The keystream is based on the key and nonce, if they are fixed, the keystream is always the same. All you need to do is XOR known or chosen plaintext into the matching ciphertext to recover the keystream
$endgroup$
– Richie Frame
Aug 29 '18 at 0:40
$begingroup$
"if the nonce is known I can do an encryption of plain text and get the same ciphered text result" If the nonce is known, you can encrypt null bytes and recover the keystream, and every message that used that nonce is now decrypted
$endgroup$
– Richie Frame
Aug 28 '18 at 10:13
$begingroup$
"if the nonce is known I can do an encryption of plain text and get the same ciphered text result" If the nonce is known, you can encrypt null bytes and recover the keystream, and every message that used that nonce is now decrypted
$endgroup$
– Richie Frame
Aug 28 '18 at 10:13
$begingroup$
@RichieFrame How do you recover the keystream?
$endgroup$
– PhillyNJ
Aug 28 '18 at 10:28
$begingroup$
@RichieFrame How do you recover the keystream?
$endgroup$
– PhillyNJ
Aug 28 '18 at 10:28
1
1
$begingroup$
CCM mode generates a keystream and XORs it with the plaintext. The keystream is based on the key and nonce, if they are fixed, the keystream is always the same. All you need to do is XOR known or chosen plaintext into the matching ciphertext to recover the keystream
$endgroup$
– Richie Frame
Aug 29 '18 at 0:40
$begingroup$
CCM mode generates a keystream and XORs it with the plaintext. The keystream is based on the key and nonce, if they are fixed, the keystream is always the same. All you need to do is XOR known or chosen plaintext into the matching ciphertext to recover the keystream
$endgroup$
– Richie Frame
Aug 29 '18 at 0:40
add a comment |
2 Answers
2
active
oldest
votes
$begingroup$
Is this attack plausible using a modern PC?
No. For AES-128 (or any secure 128-bit symmetric cipher for that matter), there are $2^128$ possible keys. You would have to try on average half of those keys before finding the right one, which is $2^128/2=2^127$. At $100,000,000$ attempts per second (or around $2^26$), it would take around $2^101$ second. The universe is around 13.7 billion years old (about $2^59$ seconds). So the amount of time it would take you is $2^42$ times the age of the universe.
There are other ways you can calculate this, but the end result is the same. See How much would it cost in U.S. dollars to brute force a 256 bit key in a year?.
Finally, the relevant XKCD:
edited Aug 28 '18 at 12:18
Jacob Bundgaard
1032
answered Aug 27 '18 at 15:31
mikeazomikeazo
33.2k789146
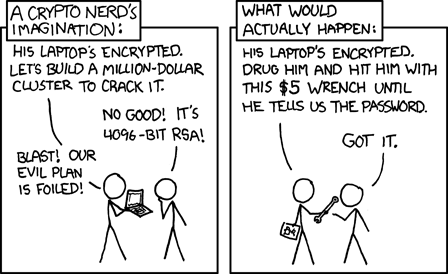
$endgroup$
5
$begingroup$
Might be worth a small sidenote that this of course generalizes to all ciphers with the specific key length; not just AES-128, but any cipher with a 128-bit key. The exact amount of time needed per key (and thus the number of keys testable per second) will vary with the complexity of the key schedule (Blowfish, I'm looking at you), but at the scales we're discussing here, that doesn't really substantially change anything. A few powers of ten more or less won't make any substantial difference.
$endgroup$
– a CVn
Aug 27 '18 at 16:49
2
$begingroup$
@MichaelKjörling "this of course generalizes to all ciphers with ... a 128-bit key" - only to symmetric ciphers that are not mathematically broken (yet). RSA needs 2048 to 4096 bits to be secure.
$endgroup$
– Alexander
Aug 27 '18 at 19:41
$begingroup$
@Alexander, agreed, but I'm not sure I understand why you are invoking RSA here. RSA is asymmetric, not symmetric. Maybe a better comparison would be Vigenere. You could have a Vigenere cipher with 128 bit key, but it would not be secure and would be much easier to break.
$endgroup$
– mikeazo
Aug 27 '18 at 19:44
$begingroup$
Good points both mikeazo and @Alexander. In my defense, I was beginning to run out of space in the margin, and I was addressing my comment primarily to mikeazo as a suggestion for an improvement to the answer.
$endgroup$
– a CVn
Aug 27 '18 at 19:48
1
$begingroup$
@PaŭloEbermann, I agree, but I wasn't completely sure what the best number would be. Besides, what's a couple of orders of magnitude among friends?
$endgroup$
– mikeazo
Aug 28 '18 at 0:40
|
show 2 more comments
$begingroup$
in a universe of combinations you can give luck and find the correct one in 1 minute. It is not mandatory to scroll through the range to find the correct key. But you can't get luck too :-)
answered Aug 28 '18 at 17:00
Luis Anderson Cerino PiresLuis Anderson Cerino Pires
1
$endgroup$
add a comment |
Your Answer
StackExchange.ifUsing("editor", function ()
return StackExchange.using("mathjaxEditing", function ()
StackExchange.MarkdownEditor.creationCallbacks.add(function (editor, postfix)
StackExchange.mathjaxEditing.prepareWmdForMathJax(editor, postfix, [["$", "$"], ["\\(","\\)"]]);
);
);
, "mathjax-editing");
StackExchange.ready(function()
var channelOptions =
tags: "".split(" "),
id: "281"
;
initTagRenderer("".split(" "), "".split(" "), channelOptions);
StackExchange.using("externalEditor", function()
// Have to fire editor after snippets, if snippets enabled
if (StackExchange.settings.snippets.snippetsEnabled)
StackExchange.using("snippets", function()
createEditor();
);
else
createEditor();
);
function createEditor()
StackExchange.prepareEditor(
heartbeatType: 'answer',
autoActivateHeartbeat: false,
convertImagesToLinks: false,
noModals: true,
showLowRepImageUploadWarning: true,
reputationToPostImages: null,
bindNavPrevention: true,
postfix: "",
imageUploader:
brandingHtml: "Powered by u003ca class="icon-imgur-white" href="https://imgur.com/"u003eu003c/au003e",
contentPolicyHtml: "User contributions licensed under u003ca href="https://creativecommons.org/licenses/by-sa/3.0/"u003ecc by-sa 3.0 with attribution requiredu003c/au003e u003ca href="https://stackoverflow.com/legal/content-policy"u003e(content policy)u003c/au003e",
allowUrls: true
,
noCode: true, onDemand: true,
discardSelector: ".discard-answer"
,immediatelyShowMarkdownHelp:true
);
);
Sign up or log in
StackExchange.ready(function ()
StackExchange.helpers.onClickDraftSave('#login-link');
);
Sign up using Google
Sign up using Facebook
Sign up using Email and Password
Post as a guest
Required, but never shown
StackExchange.ready(
function ()
StackExchange.openid.initPostLogin('.new-post-login', 'https%3a%2f%2fcrypto.stackexchange.com%2fquestions%2f61795%2fcalculate-all-possible-keys-for-aes-128-encryption-to-exploit-hardware-encryptio%23new-answer', 'question_page');
);
Post as a guest
Required, but never shown
2 Answers
2
active
oldest
votes
2 Answers
2
active
oldest
votes
active
oldest
votes
active
oldest
votes
$begingroup$
Is this attack plausible using a modern PC?
No. For AES-128 (or any secure 128-bit symmetric cipher for that matter), there are $2^128$ possible keys. You would have to try on average half of those keys before finding the right one, which is $2^128/2=2^127$. At $100,000,000$ attempts per second (or around $2^26$), it would take around $2^101$ second. The universe is around 13.7 billion years old (about $2^59$ seconds). So the amount of time it would take you is $2^42$ times the age of the universe.
There are other ways you can calculate this, but the end result is the same. See How much would it cost in U.S. dollars to brute force a 256 bit key in a year?.
Finally, the relevant XKCD:
edited Aug 28 '18 at 12:18
Jacob Bundgaard
1032
answered Aug 27 '18 at 15:31
mikeazomikeazo
33.2k789146
$endgroup$
5
$begingroup$
Might be worth a small sidenote that this of course generalizes to all ciphers with the specific key length; not just AES-128, but any cipher with a 128-bit key. The exact amount of time needed per key (and thus the number of keys testable per second) will vary with the complexity of the key schedule (Blowfish, I'm looking at you), but at the scales we're discussing here, that doesn't really substantially change anything. A few powers of ten more or less won't make any substantial difference.
$endgroup$
– a CVn
Aug 27 '18 at 16:49
2
$begingroup$
@MichaelKjörling "this of course generalizes to all ciphers with ... a 128-bit key" - only to symmetric ciphers that are not mathematically broken (yet). RSA needs 2048 to 4096 bits to be secure.
$endgroup$
– Alexander
Aug 27 '18 at 19:41
$begingroup$
@Alexander, agreed, but I'm not sure I understand why you are invoking RSA here. RSA is asymmetric, not symmetric. Maybe a better comparison would be Vigenere. You could have a Vigenere cipher with 128 bit key, but it would not be secure and would be much easier to break.
$endgroup$
– mikeazo
Aug 27 '18 at 19:44
$begingroup$
Good points both mikeazo and @Alexander. In my defense, I was beginning to run out of space in the margin, and I was addressing my comment primarily to mikeazo as a suggestion for an improvement to the answer.
$endgroup$
– a CVn
Aug 27 '18 at 19:48
1
$begingroup$
@PaŭloEbermann, I agree, but I wasn't completely sure what the best number would be. Besides, what's a couple of orders of magnitude among friends?
$endgroup$
– mikeazo
Aug 28 '18 at 0:40
|
show 2 more comments
$begingroup$
Is this attack plausible using a modern PC?
No. For AES-128 (or any secure 128-bit symmetric cipher for that matter), there are $2^128$ possible keys. You would have to try on average half of those keys before finding the right one, which is $2^128/2=2^127$. At $100,000,000$ attempts per second (or around $2^26$), it would take around $2^101$ second. The universe is around 13.7 billion years old (about $2^59$ seconds). So the amount of time it would take you is $2^42$ times the age of the universe.
There are other ways you can calculate this, but the end result is the same. See How much would it cost in U.S. dollars to brute force a 256 bit key in a year?.
Finally, the relevant XKCD:
edited Aug 28 '18 at 12:18
Jacob Bundgaard
1032
answered Aug 27 '18 at 15:31
mikeazomikeazo
33.2k789146
$endgroup$
5
$begingroup$
Might be worth a small sidenote that this of course generalizes to all ciphers with the specific key length; not just AES-128, but any cipher with a 128-bit key. The exact amount of time needed per key (and thus the number of keys testable per second) will vary with the complexity of the key schedule (Blowfish, I'm looking at you), but at the scales we're discussing here, that doesn't really substantially change anything. A few powers of ten more or less won't make any substantial difference.
$endgroup$
– a CVn
Aug 27 '18 at 16:49
2
$begingroup$
@MichaelKjörling "this of course generalizes to all ciphers with ... a 128-bit key" - only to symmetric ciphers that are not mathematically broken (yet). RSA needs 2048 to 4096 bits to be secure.
$endgroup$
– Alexander
Aug 27 '18 at 19:41
$begingroup$
@Alexander, agreed, but I'm not sure I understand why you are invoking RSA here. RSA is asymmetric, not symmetric. Maybe a better comparison would be Vigenere. You could have a Vigenere cipher with 128 bit key, but it would not be secure and would be much easier to break.
$endgroup$
– mikeazo
Aug 27 '18 at 19:44
$begingroup$
Good points both mikeazo and @Alexander. In my defense, I was beginning to run out of space in the margin, and I was addressing my comment primarily to mikeazo as a suggestion for an improvement to the answer.
$endgroup$
– a CVn
Aug 27 '18 at 19:48
1
$begingroup$
@PaŭloEbermann, I agree, but I wasn't completely sure what the best number would be. Besides, what's a couple of orders of magnitude among friends?
$endgroup$
– mikeazo
Aug 28 '18 at 0:40
|
show 2 more comments
$begingroup$
Is this attack plausible using a modern PC?
No. For AES-128 (or any secure 128-bit symmetric cipher for that matter), there are $2^128$ possible keys. You would have to try on average half of those keys before finding the right one, which is $2^128/2=2^127$. At $100,000,000$ attempts per second (or around $2^26$), it would take around $2^101$ second. The universe is around 13.7 billion years old (about $2^59$ seconds). So the amount of time it would take you is $2^42$ times the age of the universe.
There are other ways you can calculate this, but the end result is the same. See How much would it cost in U.S. dollars to brute force a 256 bit key in a year?.
Finally, the relevant XKCD:
edited Aug 28 '18 at 12:18
Jacob Bundgaard
1032
answered Aug 27 '18 at 15:31
mikeazomikeazo
33.2k789146
$endgroup$
Is this attack plausible using a modern PC?
No. For AES-128 (or any secure 128-bit symmetric cipher for that matter), there are $2^128$ possible keys. You would have to try on average half of those keys before finding the right one, which is $2^128/2=2^127$. At $100,000,000$ attempts per second (or around $2^26$), it would take around $2^101$ second. The universe is around 13.7 billion years old (about $2^59$ seconds). So the amount of time it would take you is $2^42$ times the age of the universe.
There are other ways you can calculate this, but the end result is the same. See How much would it cost in U.S. dollars to brute force a 256 bit key in a year?.
Finally, the relevant XKCD:
edited Aug 28 '18 at 12:18
Jacob Bundgaard
1032
answered Aug 27 '18 at 15:31
mikeazomikeazo
33.2k789146
edited Aug 28 '18 at 12:18
Jacob Bundgaard
1032
edited Aug 28 '18 at 12:18
Jacob Bundgaard
1032
edited Aug 28 '18 at 12:18
Jacob Bundgaard
1032
1032
answered Aug 27 '18 at 15:31
mikeazomikeazo
33.2k789146
answered Aug 27 '18 at 15:31
mikeazomikeazo
33.2k789146
answered Aug 27 '18 at 15:31
mikeazomikeazo
33.2k789146
33.2k789146
5
$begingroup$
Might be worth a small sidenote that this of course generalizes to all ciphers with the specific key length; not just AES-128, but any cipher with a 128-bit key. The exact amount of time needed per key (and thus the number of keys testable per second) will vary with the complexity of the key schedule (Blowfish, I'm looking at you), but at the scales we're discussing here, that doesn't really substantially change anything. A few powers of ten more or less won't make any substantial difference.
$endgroup$
– a CVn
Aug 27 '18 at 16:49
2
$begingroup$
@MichaelKjörling "this of course generalizes to all ciphers with ... a 128-bit key" - only to symmetric ciphers that are not mathematically broken (yet). RSA needs 2048 to 4096 bits to be secure.
$endgroup$
– Alexander
Aug 27 '18 at 19:41
$begingroup$
@Alexander, agreed, but I'm not sure I understand why you are invoking RSA here. RSA is asymmetric, not symmetric. Maybe a better comparison would be Vigenere. You could have a Vigenere cipher with 128 bit key, but it would not be secure and would be much easier to break.
$endgroup$
– mikeazo
Aug 27 '18 at 19:44
$begingroup$
Good points both mikeazo and @Alexander. In my defense, I was beginning to run out of space in the margin, and I was addressing my comment primarily to mikeazo as a suggestion for an improvement to the answer.
$endgroup$
– a CVn
Aug 27 '18 at 19:48
1
$begingroup$
@PaŭloEbermann, I agree, but I wasn't completely sure what the best number would be. Besides, what's a couple of orders of magnitude among friends?
$endgroup$
– mikeazo
Aug 28 '18 at 0:40
|
show 2 more comments
5
$begingroup$
Might be worth a small sidenote that this of course generalizes to all ciphers with the specific key length; not just AES-128, but any cipher with a 128-bit key. The exact amount of time needed per key (and thus the number of keys testable per second) will vary with the complexity of the key schedule (Blowfish, I'm looking at you), but at the scales we're discussing here, that doesn't really substantially change anything. A few powers of ten more or less won't make any substantial difference.
$endgroup$
– a CVn
Aug 27 '18 at 16:49
2
$begingroup$
@MichaelKjörling "this of course generalizes to all ciphers with ... a 128-bit key" - only to symmetric ciphers that are not mathematically broken (yet). RSA needs 2048 to 4096 bits to be secure.
$endgroup$
– Alexander
Aug 27 '18 at 19:41
$begingroup$
@Alexander, agreed, but I'm not sure I understand why you are invoking RSA here. RSA is asymmetric, not symmetric. Maybe a better comparison would be Vigenere. You could have a Vigenere cipher with 128 bit key, but it would not be secure and would be much easier to break.
$endgroup$
– mikeazo
Aug 27 '18 at 19:44
$begingroup$
Good points both mikeazo and @Alexander. In my defense, I was beginning to run out of space in the margin, and I was addressing my comment primarily to mikeazo as a suggestion for an improvement to the answer.
$endgroup$
– a CVn
Aug 27 '18 at 19:48
1
$begingroup$
@PaŭloEbermann, I agree, but I wasn't completely sure what the best number would be. Besides, what's a couple of orders of magnitude among friends?
$endgroup$
– mikeazo
Aug 28 '18 at 0:40
5
5
$begingroup$
Might be worth a small sidenote that this of course generalizes to all ciphers with the specific key length; not just AES-128, but any cipher with a 128-bit key. The exact amount of time needed per key (and thus the number of keys testable per second) will vary with the complexity of the key schedule (Blowfish, I'm looking at you), but at the scales we're discussing here, that doesn't really substantially change anything. A few powers of ten more or less won't make any substantial difference.
$endgroup$
– a CVn
Aug 27 '18 at 16:49
$begingroup$
Might be worth a small sidenote that this of course generalizes to all ciphers with the specific key length; not just AES-128, but any cipher with a 128-bit key. The exact amount of time needed per key (and thus the number of keys testable per second) will vary with the complexity of the key schedule (Blowfish, I'm looking at you), but at the scales we're discussing here, that doesn't really substantially change anything. A few powers of ten more or less won't make any substantial difference.
$endgroup$
– a CVn
Aug 27 '18 at 16:49
2
2
$begingroup$
@MichaelKjörling "this of course generalizes to all ciphers with ... a 128-bit key" - only to symmetric ciphers that are not mathematically broken (yet). RSA needs 2048 to 4096 bits to be secure.
$endgroup$
– Alexander
Aug 27 '18 at 19:41
$begingroup$
@MichaelKjörling "this of course generalizes to all ciphers with ... a 128-bit key" - only to symmetric ciphers that are not mathematically broken (yet). RSA needs 2048 to 4096 bits to be secure.
$endgroup$
– Alexander
Aug 27 '18 at 19:41
$begingroup$
@Alexander, agreed, but I'm not sure I understand why you are invoking RSA here. RSA is asymmetric, not symmetric. Maybe a better comparison would be Vigenere. You could have a Vigenere cipher with 128 bit key, but it would not be secure and would be much easier to break.
$endgroup$
– mikeazo
Aug 27 '18 at 19:44
$begingroup$
@Alexander, agreed, but I'm not sure I understand why you are invoking RSA here. RSA is asymmetric, not symmetric. Maybe a better comparison would be Vigenere. You could have a Vigenere cipher with 128 bit key, but it would not be secure and would be much easier to break.
$endgroup$
– mikeazo
Aug 27 '18 at 19:44
$begingroup$
Good points both mikeazo and @Alexander. In my defense, I was beginning to run out of space in the margin, and I was addressing my comment primarily to mikeazo as a suggestion for an improvement to the answer.
$endgroup$
– a CVn
Aug 27 '18 at 19:48
$begingroup$
Good points both mikeazo and @Alexander. In my defense, I was beginning to run out of space in the margin, and I was addressing my comment primarily to mikeazo as a suggestion for an improvement to the answer.
$endgroup$
– a CVn
Aug 27 '18 at 19:48
1
1
$begingroup$
@PaŭloEbermann, I agree, but I wasn't completely sure what the best number would be. Besides, what's a couple of orders of magnitude among friends?
$endgroup$
– mikeazo
Aug 28 '18 at 0:40
$begingroup$
@PaŭloEbermann, I agree, but I wasn't completely sure what the best number would be. Besides, what's a couple of orders of magnitude among friends?
$endgroup$
– mikeazo
Aug 28 '18 at 0:40
|
show 2 more comments
$begingroup$
in a universe of combinations you can give luck and find the correct one in 1 minute. It is not mandatory to scroll through the range to find the correct key. But you can't get luck too :-)
answered Aug 28 '18 at 17:00
Luis Anderson Cerino PiresLuis Anderson Cerino Pires
1
$endgroup$
add a comment |
$begingroup$
in a universe of combinations you can give luck and find the correct one in 1 minute. It is not mandatory to scroll through the range to find the correct key. But you can't get luck too :-)
answered Aug 28 '18 at 17:00
Luis Anderson Cerino PiresLuis Anderson Cerino Pires
1
$endgroup$
add a comment |
$begingroup$
in a universe of combinations you can give luck and find the correct one in 1 minute. It is not mandatory to scroll through the range to find the correct key. But you can't get luck too :-)
answered Aug 28 '18 at 17:00
Luis Anderson Cerino PiresLuis Anderson Cerino Pires
1
$endgroup$
in a universe of combinations you can give luck and find the correct one in 1 minute. It is not mandatory to scroll through the range to find the correct key. But you can't get luck too :-)
answered Aug 28 '18 at 17:00
Luis Anderson Cerino PiresLuis Anderson Cerino Pires
1
answered Aug 28 '18 at 17:00
Luis Anderson Cerino PiresLuis Anderson Cerino Pires
1
answered Aug 28 '18 at 17:00
Luis Anderson Cerino PiresLuis Anderson Cerino Pires
1
answered Aug 28 '18 at 17:00
Luis Anderson Cerino PiresLuis Anderson Cerino Pires
1
1
add a comment |
add a comment |
Thanks for contributing an answer to Cryptography Stack Exchange!
- Please be sure to answer the question. Provide details and share your research!
But avoid …
- Asking for help, clarification, or responding to other answers.
- Making statements based on opinion; back them up with references or personal experience.
Use MathJax to format equations. MathJax reference.
To learn more, see our tips on writing great answers.
Sign up or log in
StackExchange.ready(function ()
StackExchange.helpers.onClickDraftSave('#login-link');
);
Sign up using Google
Sign up using Facebook
Sign up using Email and Password
Post as a guest
Required, but never shown
StackExchange.ready(
function ()
StackExchange.openid.initPostLogin('.new-post-login', 'https%3a%2f%2fcrypto.stackexchange.com%2fquestions%2f61795%2fcalculate-all-possible-keys-for-aes-128-encryption-to-exploit-hardware-encryptio%23new-answer', 'question_page');
);
Post as a guest
Required, but never shown
Sign up or log in
StackExchange.ready(function ()
StackExchange.helpers.onClickDraftSave('#login-link');
);
Sign up using Google
Sign up using Facebook
Sign up using Email and Password
Post as a guest
Required, but never shown
Sign up or log in
StackExchange.ready(function ()
StackExchange.helpers.onClickDraftSave('#login-link');
);
Sign up using Google
Sign up using Facebook
Sign up using Email and Password
Post as a guest
Required, but never shown
Sign up or log in
StackExchange.ready(function ()
StackExchange.helpers.onClickDraftSave('#login-link');
);
Sign up using Google
Sign up using Facebook
Sign up using Email and Password
Sign up using Google
Sign up using Facebook
Sign up using Email and Password
Post as a guest
Required, but never shown
Required, but never shown
Required, but never shown
Required, but never shown
Required, but never shown
Required, but never shown
Required, but never shown
Required, but never shown
Required, but never shown
$begingroup$
"if the nonce is known I can do an encryption of plain text and get the same ciphered text result" If the nonce is known, you can encrypt null bytes and recover the keystream, and every message that used that nonce is now decrypted
$endgroup$
– Richie Frame
Aug 28 '18 at 10:13
$begingroup$
@RichieFrame How do you recover the keystream?
$endgroup$
– PhillyNJ
Aug 28 '18 at 10:28
1
$begingroup$
CCM mode generates a keystream and XORs it with the plaintext. The keystream is based on the key and nonce, if they are fixed, the keystream is always the same. All you need to do is XOR known or chosen plaintext into the matching ciphertext to recover the keystream
$endgroup$
– Richie Frame
Aug 29 '18 at 0:40