Hagen–Poiseuille equation

In nonideal fluid dynamics, the Hagen–Poiseuille equation, also known as the Hagen–Poiseuille law, Poiseuille law or Poiseuille equation, is a physical law that gives the pressure drop in an incompressible and Newtonian fluid in laminar flow flowing through a long cylindrical pipe of constant cross section.
It can be successfully applied to air flow in lung alveoli, or the flow through a drinking straw or through a hypodermic needle. It was experimentally derived independently by Jean Léonard Marie Poiseuille in 1838^[1] and Gotthilf Heinrich Ludwig Hagen,^[2] and published by Poiseuille in 1840–41 and 1846.^[1]

The assumptions of the equation are that the fluid is incompressible and Newtonian; the flow is laminar through a pipe of constant circular cross-section that is substantially longer than its diameter; and there is no acceleration of fluid in the pipe. For velocities and pipe diameters above a threshold, actual fluid flow is not laminar but turbulent, leading to larger pressure drops than calculated by the Hagen–Poiseuille equation.

Equation[edit]

In standard fluid-kinetics notation:^[3]^[4]^[5]

displaystyle Delta P=frac 8mu LQpi R^4

where:

Δ P

is the pressure difference between the two ends,

L

is the length of pipe,

μ

is the dynamic viscosity,

Q

is the volumetric flow rate,

R

is the pipe radius.

The equation does not hold close to the pipe entrance.^[6]^:3

The equation fails in the limit of low viscosity, wide and/or short pipe. Low viscosity or a wide pipe may result in turbulent flow, making it necessary to use more complex models, such as Darcy–Weisbach equation. If the pipe is too short, the Hagen–Poiseuille equation may result in unphysically high flow rates; the flow is bounded by Bernoulli's principle, under less restrictive conditions, by

displaystyle Q_max =pi R^2sqrt frac 2Delta Prho .

Relation to Darcy–Weisbach[edit]

Normally, Hagen-Poiseuille flow implies not just the relation for the pressure drop, above, but also the full solution for the laminar flow profile, which is parabolic. However, the result for the pressure drop can be extended to turbulent flow by inferring an effective turbulent viscosity in the case of turbulent flow, even though the flow profile in turbulent flow is strictly speaking not actually parabolic. In both cases, laminar or turbulent, the pressure drop is related to the stress at the wall, which determines the so-called friction factor. The wall stress can be determined phenomenologically by the Darcy–Weisbach equation in the field of hydraulics, given a relationship for the friction factor in terms of the Reynolds number. In the case of laminar flow, for a circular cross section:

displaystyle Lambda =frac 64mathrm Re ,quad mathrm Re =frac rho vdmu ,

where $Re$ is the Reynolds number, $ρ$ is the fluid density, $v$ is the mean flow velocity, which is half the maximal flow velocity in the case of laminar flow. It proves more useful to define the Reynolds number in terms of the mean flow velocity because this quantity remains well defined even in the case of turbulent flow, whereas the maximal flow velocity may not be, or in any case, it may be difficult to infer. In this form the law approximates the Darcy friction factor, the energy (head) loss factor, friction loss factor or Darcy (friction) factor $Λ$ in the laminar flow at very low velocities in cylindrical tube. The theoretical derivation of a slightly different form of the law was made independently by Wiedman in 1856 and Neumann and E. Hagenbach in 1858 (1859, 1860). Hagenbach was the first who called this law the Poiseuille's law.

The law is also very important in hemorheology and hemodynamics, both fields of physiology.^[7]

Poiseuille's law was later in 1891 extended to turbulent flow by L. R. Wilberforce, based on Hagenbach's work.

Derivation[edit]

The Hagen–Poiseuille equation can be derived from the Navier–Stokes equations. Although more lengthy than directly using the Navier–Stokes equations, an alternative method of deriving the Hagen–Poiseuille equation is as follows.

Liquid flow through a pipe[edit]

a) A tube showing the imaginary lamina. b) A cross section of the tube shows the lamina moving at different speeds. Those closest to the edge of the tube are moving slowly while those near the center are moving quickly.

Assume the liquid exhibits laminar flow. Laminar flow in a round pipe prescribes that there are a bunch of circular layers (lamina) of liquid, each having a velocity determined only by their radial distance from the center of the tube. Also assume the center is moving fastest while the liquid touching the walls of the tube is stationary (due to the no-slip condition).

To figure out the motion of the liquid, all forces acting on each lamina must be known:

The pressure force pushing the liquid through the tube is the change in pressure multiplied by the area: $F = - A Δ P$ . This force is in the direction of the motion of the liquid. The negative sign comes from the conventional way we define $Δ P = P end - P top < 0$ .

Viscosity effects will pull from the faster lamina immediately closer to the center of the tube.

Viscosity effects will drag from the slower lamina immediately closer to the walls of the tube.

Viscosity[edit]

Two fluids moving past each other in the

x

direction. The liquid on top is moving faster and will be pulled in the negative direction by the bottom liquid while the bottom liquid will be pulled in the positive direction by the top liquid.

When two layers of liquid in contact with each other move at different speeds, there will be a shear force between them. This force is proportional to the area of contact $A$ , the velocity gradient perpendicular to the direction of flow $Δ v x / Δ y$ , and a proportionality constant (viscosity) and is given by

displaystyle F_textviscosity, top=-mu Afrac Delta v_xDelta y.

The negative sign is in there because we are concerned with the faster moving liquid (top in figure), which is being slowed by the slower liquid (bottom in figure). By Newton's third law of motion, the force on the slower liquid is equal and opposite (no negative sign) to the force on the faster liquid. This equation assumes that the area of contact is so large that we can ignore any effects from the edges and that the fluids behave as Newtonian fluids.

Faster lamina[edit]

Assume that we are figuring out the force on the lamina with radius $r$ . From the equation above, we need to know the area of contact and the velocity gradient. Think of the lamina as a ring of radius $r$ , thickness $dr$ , and length $Δ x$ . The area of contact between the lamina and the faster one is simply the area of the inside of the cylinder: $A = 2π r Δ x$ . We don't know the exact form for the velocity of the liquid within the tube yet, but we do know (from our assumption above) that it is dependent on the radius. Therefore, the velocity gradient is the change of the velocity with respect to the change in the radius at the intersection of these two laminae. That intersection is at a radius of $r$ . So, considering that this force will be positive with respect to the movement of the liquid (but the derivative of the velocity is negative), the final form of the equation becomes

displaystyle F_textviscosity, fast=-2pi rmu ,Delta x,left.frac dvdrright

where the vertical bar and subscript $r$ following the derivative indicates that it should be taken at a radius of $r$ .

Slower lamina[edit]

Next let's find the force of drag from the slower lamina. We need to calculate the same values that we did for the force from the faster lamina. In this case, the area of contact is at $r + dr$ instead of $r$ . Also, we need to remember that this force opposes the direction of movement of the liquid and will therefore be negative (and that the derivative of the velocity is negative).

displaystyle F_textviscosity, slow=2pi (r+dr)mu ,Delta xleft.frac dvdrright

Putting it all together[edit]

To find the solution for the flow of a laminar layer through a tube, we need to make one last assumption. There is no acceleration of liquid in the pipe, and by Newton's first law, there is no net force. If there is no net force then we can add all of the forces together to get zero

displaystyle 0=F_textpressure+F_textviscosity, fast+F_textviscosity, slow

or

_r+2pi (r+dr)mu ,Delta x,left.frac dvdrrightvert _r+dr.

First, to get everything happening at the same point, use the first two terms of a Taylor series expansion of the velocity gradient:

_r+dr=left.frac dvdrright

The expression is valid for all laminae. Grouping like terms and dropping the vertical bar since all derivatives are assumed to be at radius $r$ ,

displaystyle 0=Delta P2pi r,dr+2pi mu ,dr,Delta xfrac dvdr+2pi rmu ,dr,Delta xfrac d^2vdr^2+2pi mu (dr)^2,Delta xfrac d^2vdr^2.

Finally, put this expression in the form of a differential equation, dropping the term quadratic in $dr$ .

displaystyle frac 1mu frac Delta PDelta x=frac d^2vdr^2+frac 1rfrac dvdr

It can be seen that both sides of the equations are negative: there is a drop of pressure along the tube (left side) and both first and second derivatives of the velocity are negative (velocity has a maximum value at the center of the tube, where $r = 0)$ . Using the product rule, the equation may be rearranged to:

displaystyle frac 1mu frac Delta PDelta x=frac 1rfrac ddrleft(rfrac dvdrright).

The right-hand side is the radial term of the Laplace operator $\nabla 2$ , so this differential equation is a special case of the Poisson equation. It is subject to the following boundary conditions:

$displaystyle v(r)=0quad mbox at r=R$	— "no-slip" boundary condition at the wall
$displaystyle frac dvdr=0quad mbox at r=0$	— axial symmetry.

Axial symmetry means that the velocity $v (r)$ is maximum at the center of the tube, therefore the first derivative $dv / dr$ is zero at $r = 0$ .

The differential equation can be integrated to:

displaystyle v(r)=frac 14mu r^2frac Delta PDelta x+Aln(r)+B.

To find $A$ and $B$ , we use the boundary conditions.

First, the symmetry boundary condition indicates:

displaystyle frac dvdr=frac 12mu rfrac Delta PDelta x+frac Ar=0quad mbox at r=0.

A solution possible only if $A = 0$ . Next the no-slip boundary condition is applied to the remaining equation:

displaystyle v(R)=frac 14mu R^2frac Delta PDelta x+B=0

so therefore

displaystyle B=-frac 14mu R^2frac Delta PDelta x.

Now we have a formula for the velocity of liquid moving through the tube as a function of the distance from the center of the tube

displaystyle v=-frac 14mu frac Delta PDelta x(R^2-r^2)

or, at the center of the tube where the liquid is moving fastest ( $r = 0$ ) with $R$ being the radius of the tube,

displaystyle v_max=-frac 14mu frac Delta PDelta xR^2.

Poiseuille's law[edit]

To get the total volume that flows through the tube, we need to add up the contributions from each lamina. To calculate the flow through each lamina, we multiply the velocity (from above) and the area of the lamina.

displaystyle Q(r),dr=-frac 14mu frac Delta PDelta x(R^2-r^2)2pi r,dr=-frac pi 2mu frac Delta PDelta x(rR^2-r^3),dr

Finally, we integrate over all lamina via the radius variable $r$ .

displaystyle Q=-frac pi 2mu frac Delta PDelta xint _0^R(rR^2-r^3),dr=-frac Delta Ppi R^48mu Delta x

Startup of Poiseuille flow in a pipe^[8][edit]

When a constant pressure gradient $displaystyle G=-dp/dx=textconstant$ is applied between two ends of a long pipe, the flow will not immediately obtain Poiseuille profile, rather it develops through time and reaches the Poiseuille profile at steady state. The Navier-Stokes equations reduce to

displaystyle frac partial upartial t=frac Grho +nu left(frac partial ^2upartial r^2+frac 1rfrac partial upartial rright)

with initial and boundary conditions,

displaystyle u(r,0)=0,quad u(R,t)=0.

The velocity distribution is given by

displaystyle u(r,t)=frac G4mu (R^2-r^2)-frac 2GR^2mu sum _n=1^infty frac 1lambda _n^3frac J_o(lambda _nr/R)J_1(lambda _n)e^-lambda _n^2frac nu tR^2,quad J_o(lambda _n)=0

where $displaystyle J_o(lambda _nr/R)$ is the Bessel function of the first kind of order zero and $lambda _n$ are the positive roots of this function and $displaystyle J_1(lambda _n)$ is the Bessel function of the first kind of order one. As $trightarrow infty$ , Poiseuille solution is recovered.

Poiseuille flow in annular section^[9][edit]

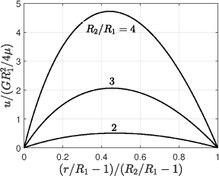
Poiseuille flow in annular section

If $R_1$ is the inner cylinder radii and $R_2$ is the outer cylinder radii, with applied pressure gradient between the two ends $displaystyle G=-dp/dx=textconstant$ , the velocity distribution and the volume flux through the annular pipe are

displaystyle beginalignedu(r)&=frac G4mu (R_1^2-r^2)+frac G4mu (R_2^2-R_1^2)frac ln(r/R_1)ln(R_2/R_1),\Q&=frac Gpi 8mu left[R_2^4-R_1^4-frac (R_2^2-R_1^2)^2ln R_2/R_1right].endaligned

When $displaystyle R_2=R, R_1=0$ , the original problem is recovered.

Plane Poiseuille flow[edit]

Plane Poiseuille flow

Plane Poiseuille flow is flow created between two infinitely long parallel plates, separated by a distance $h$ with a constant pressure gradient $displaystyle G=-dp/dx=textconstant$ is applied in the direction of flow. The flow is essentially unidirectional because of infinite length. The Navier-Stokes equations reduce to

displaystyle frac d^2udy^2=-frac Gmu

with no-slip condition on both walls

displaystyle u(0)=0,quad u(h)=0

Therefore, the velocity distribution and the volume flow rate per unit length are

displaystyle u(y)=frac G2mu y(h-y),quad Q=frac Gh^312mu .

Poiseuille flow through some non-circular cross-sections^[10][edit]

Joseph Boussinesq^[11] derived the velocity profile and volume flow rate in 1868 for rectangular channel and tubes of equilateral triangular cross-section and for elliptical cross-section. Joseph Proudman^[12] derived the same for isosceles triangles in 1914. Let $displaystyle G=-dp/dx=textconstant$ be the constant pressure gradient acting in direction parallel to the motion.

The velocity and the volume flow rate in a rectangular channel of height $displaystyle 0leq yleq h$ and width $displaystyle 0leq zleq l$ are

displaystyle beginalignedu(y,z)&=frac G2mu y(h-y)-frac 4Gh^2mu pi ^3sum _n=1^infty frac 1(2n-1)^3frac sinh(beta _nz)+sinh(beta _n(l-z))sinh(beta _nl)sin(beta _ny),quad beta _n=frac (2n-1)pi h,\Q&=frac Gh^3l12mu -frac 16Gh^4pi ^5mu sum _n=1^infty frac 1(2n-1)^5frac cosh(beta _nl)-1sinh(beta _nl).endaligned

The velocity and the volume flow rate of tube with equilateral triangular cross-section of side length $displaystyle 2h/sqrt 3$ are

displaystyle beginalignedu(y,z)&=-frac G4mu h(y-h)(y^2-3z^2),\Q&=frac Gh^460sqrt 3mu .endaligned

The velocity and the volume flow rate in the right-angled isosceles triangle $displaystyle y=pi , ypm z=0$ are

displaystyle beginalignedu(y,z)&=frac G2mu (y+z)(pi -y)-frac Gpi mu sum _n=1^infty frac 1beta _n^3sinh(2pi beta _n)sinh[beta _n(2pi -y+z)]sin[beta _n(y+z)]-sinh[beta _n(y+z)]sin[beta _n(y-z)],quad beta _n=n-frac 12,\Q&=frac Gpi ^412mu -frac G2pi mu sum _n=1^infty frac 1beta _n^5[coth(2pi beta _n)+csc(2pi beta _n)].endaligned

The velocity distribution for tubes of elliptical cross-section with semi-axis $a$ and $b$ is^[8]

displaystyle beginalignedu(y,z)&=frac G2mu left(frac 1a^2+frac 1b^2right)left(1-frac y^2a^2-frac z^2b^2right),\Q&=frac pi Ga^3b^34mu (a^2+b^2).endaligned

Here, when $a=b$ , Poiseuille flow for circular pipe is recovered and when $arightarrowinfty$ , plane Poiseuille flow is recovered.

Poiseuille flow through arbitrary cross-section[edit]

The flow through arbitrary cross-section $displaystyle u(y,z)$ satisfies the condition that $u=0$ on the walls. The governing equation reduces to^[13]

displaystyle frac partial ^2upartial y^2+frac partial ^2upartial z^2=-frac Gmu .

If we introduce a new dependent variable as

displaystyle U=u+frac G4mu (y^2+z^2),

then it is easy to see that the problem reduces to that integrating a Laplace equation

displaystyle frac partial ^2Upartial y^2+frac partial ^2Upartial z^2=0

satisfying the condition

displaystyle U=frac G4mu (y^2+z^2)

on the wall.

Poiseuille's equation for compressible fluids[edit]

For a compressible fluid in a tube the volumetric flow rate and the linear velocity are not constant along the tube. The flow is usually expressed at outlet pressure. As fluid is compressed or expands, work is done and the fluid is heated or cooled. This means that the flow rate depends on the heat transfer to and from the fluid. For an ideal gas in the isothermal case, where the temperature of the fluid is permitted to equilibrate with its surroundings, and when the pressure difference between ends of the pipe is small, the volumetric flow rate at the pipe outlet is given by

displaystyle Q=frac dVdt=vpi R^2=frac pi R^4left(P_mathrm i -P_mathrm o right)8mu Ltimes frac P_mathrm i +P_mathrm o 2P_mathrm o =frac pi R^416mu Lleft(frac P_mathrm i ^2-P_mathrm o ^2P_mathrm o right)

where:

P i

is inlet pressure

P o

is outlet pressure

L

is the length of tube

mu

is the viscosity

R

is the radius

V

is the volume of the fluid at outlet pressure

v

is the velocity of the fluid at outlet pressure

This equation can be seen as Poiseuille's law with an extra correction factor $P i + P o / 2 P o$ expressing the average pressure relative to the outlet pressure.

Electrical circuits analogy[edit]

Electricity was originally understood to be a kind of fluid. This hydraulic analogy is still conceptually useful for understanding circuits. This analogy is also used to study the frequency response of fluid-mechanical networks using circuit tools, in which case the fluid network is termed a hydraulic circuit.

Poiseuille's law corresponds to Ohm's law for electrical circuits, $V = IR$ .

Since the net force acting on the fluid is equal to

displaystyle Delta F=SDelta P,

where $S = π r 2$ , i.e. $Δ F = π r 2 Δ P$ , then from Poiseuille's law

Delta P=frac 8mu LQpi r^4

it follows that

Delta F=frac 8mu LQr^2

.

For electrical circuits, let $n$ be the concentration of free charged particles (in m⁻³) and let $q *$ be the charge of each particle (in coulombs). (For electrons, $q * = e = 6981160000000000000♠ 1.6 \times 10 -19 C$ .)

Then $nQ$ is the number of particles in the volume $Q$ , and $nQq *$ is their total charge. This is the charge that flows through the cross section per unit time, i.e. the current $I$ . Therefore, $I = nQq *$ . Consequently, $Q = I / nq *$ , and

displaystyle Delta F=frac 8mu LInr^2q^*.

But $Δ F = Eq$ , where $q$ is the total charge in the volume of the tube. The volume of the tube is equal to $π r 2 L$ , so the number of charged particles in this volume is equal to $n π r 2 L$ , and their total charge is

displaystyle q=npi r^2Lq^*.

Now,

displaystyle E=frac Delta Fq=frac 8mu In^2pi r^4(q^*)^2.

Since the voltage $V = EL$ , we get

displaystyle V=frac 8mu LIn^2pi r^4(q^*)^2.

This is exactly Ohm's law, where the resistance $R = V / I$ is described by the formula

displaystyle R=frac 8mu Ln^2pi r^4(q^*)^2

.

It follows that the resistance $R$ is proportional to the length $L$ of the resistor, which is true. However, it also follows that
the resistance $R$ is inversely proportional to the fourth power of the radius $r$ , i.e. the resistance $R$ is inversely proportional to the second power of the cross section area $S = π r 2$ of the resistor, which is wrong according to the electrical analogy.

The correct relation is

displaystyle R=frac rho LS,

where $ρ$ is the specific resistance; i.e. the resistance $R$ is inversely proportional to the cross section area $S$ of the resistor.^[14]

The reason why Poiseuille's law leads to a wrong formula for the resistance $R$ is the difference between the fluid flow and the electric current. Electron gas is inviscid, so its velocity does not depend on the distance to the walls of the conductor. The resistance is due to the interaction between the flowing electrons and the atoms of the conductor. Therefore, Poiseuille's law and the hydraulic analogy are useful only within certain limits when applied to electricity.

Both Ohm's law and Poiseuille's law illustrate transport phenomena.

Medical applications – intravenous access and fluid delivery[edit]

The Hagen–Poiseuille equation is useful in determining the flow rate of intravenous fluids that may be achieved using various sizes of peripheral and central cannulas. The equation states that flow rate is proportional to the radius to the fourth power, meaning that a small increase in the internal diameter of the cannula yields a significant increase in flow rate of IV fluids. The radius of IV cannulas is typically measured in "gauge", which is inversely proportional to the radius. Peripheral IV cannulas are typically available as (from large to small) 14G, 16G, 18G, 20G, 22G. As an example, the flow of a 14G cannula is typically twice that of a 16G, and ten times that of a 20G. It also states that flow is inversely proportional to length, meaning that longer lines have lower flow rates. This is important to remember as in an emergency, many clinicians favor shorter, larger catheters compared to longer, narrower catheters. While of less clinical importance, the change in pressure can be used to speed up flow rate by pressurizing the bag of fluid, squeezing the bag, or hanging the bag higher from the level of the cannula. It is also useful to understand that viscous fluids will flow slower (e.g. in blood transfusion).

Notes[edit]

^ ^a^b Sutera, Salvatore P.; Skalak, Richard (1993). "The History of Poiseuille's Law". Annual Review of Fluid Mechanics. 25: 1–19. Bibcode:1993AnRFM..25....1S. doi:10.1146/annurev.fl.25.010193.000245..mw-parser-output cite.citationfont-style:inherit.mw-parser-output .citation qquotes:"""""""'""'".mw-parser-output .citation .cs1-lock-free abackground:url("//upload.wikimedia.org/wikipedia/commons/thumb/6/65/Lock-green.svg/9px-Lock-green.svg.png")no-repeat;background-position:right .1em center.mw-parser-output .citation .cs1-lock-limited a,.mw-parser-output .citation .cs1-lock-registration abackground:url("//upload.wikimedia.org/wikipedia/commons/thumb/d/d6/Lock-gray-alt-2.svg/9px-Lock-gray-alt-2.svg.png")no-repeat;background-position:right .1em center.mw-parser-output .citation .cs1-lock-subscription abackground:url("//upload.wikimedia.org/wikipedia/commons/thumb/a/aa/Lock-red-alt-2.svg/9px-Lock-red-alt-2.svg.png")no-repeat;background-position:right .1em center.mw-parser-output .cs1-subscription,.mw-parser-output .cs1-registrationcolor:#555.mw-parser-output .cs1-subscription span,.mw-parser-output .cs1-registration spanborder-bottom:1px dotted;cursor:help.mw-parser-output .cs1-ws-icon abackground:url("//upload.wikimedia.org/wikipedia/commons/thumb/4/4c/Wikisource-logo.svg/12px-Wikisource-logo.svg.png")no-repeat;background-position:right .1em center.mw-parser-output code.cs1-codecolor:inherit;background:inherit;border:inherit;padding:inherit.mw-parser-output .cs1-hidden-errordisplay:none;font-size:100%.mw-parser-output .cs1-visible-errorfont-size:100%.mw-parser-output .cs1-maintdisplay:none;color:#33aa33;margin-left:0.3em.mw-parser-output .cs1-subscription,.mw-parser-output .cs1-registration,.mw-parser-output .cs1-formatfont-size:95%.mw-parser-output .cs1-kern-left,.mw-parser-output .cs1-kern-wl-leftpadding-left:0.2em.mw-parser-output .cs1-kern-right,.mw-parser-output .cs1-kern-wl-rightpadding-right:0.2em

^ István Szabó, ;;Geschichte der mechanischen Prinzipien und ihrer wichtigsten Anwendungen, Basel: Birkhäuser Verlag, 1979.

^ Kirby, B. J. (2010). Micro- and Nanoscale Fluid Mechanics: Transport in Microfluidic Devices. Cambridge University Press. ISBN 978-0-521-11903-0.

^ Bruus, H. (2007). Theoretical Microfluidics.

^ "Poiseuille and his law" (PDF). pdfs.semanticscholar.org.

^ Vogel, Steven (1981). Life in Moving Fluids: The Physical Biology of Flow. PWS Kent Publishers. ISBN 0871507498.

^ Determinants of blood vessel resistance.

^ ^a^b Batchelor, George Keith. An introduction to fluid dynamics. Cambridge university press, 2000.

^ Rosenhead, Louis, ed. Laminar boundary layers. Clarendon Press, 1963.

^ Drazin, Philip G., and Norman Riley. The Navier–Stokes equations: a classification of flows and exact solutions. No. 334. Cambridge University Press, 2006.

^ Boussinesq, Joseph. "Mémoire sur l’influence des Frottements dans les Mouvements Réguliers des Fluids." J. Math. Pures Appl 13.2 (1868): 377-424.

^ Proudman, J. "IV. Notes on the motion of viscous liquids in channels." The London, Edinburgh, and Dublin Philosophical Magazine and Journal of Science 28.163 (1914): 30-36.

^ Samuel Newby Curle and H.J. Davies. Modern Fluid Dynamics. Volume 1, Incompressible Flow, Van Nostrand Reinhold Inc (1971)

^ Fütterer, C. et al. "Injection and flow control system for microchannels" Lab-on-a-Chip (2004): 351-356.

References[edit]

Sutera, S. P.; Skalak, R. (1993). "The history of Poiseuille's law". Annual Review of Fluid Mechanics. 25: 1–19. Bibcode:1993AnRFM..25....1S. doi:10.1146/annurev.fl.25.010193.000245.

Pfitzner, J (1976). "Poiseuille and his law". Anaesthesia. 31 (2) (published Mar 1976). pp. 273–5. doi:10.1111/j.1365-2044.1976.tb11804.x. PMID 779509.

Bennett, C. O.; Myers, J. E. (1962). "Momentum, Heat, and Mass Transfer". McGraw-Hill.

External links[edit]

Poiseuille's law for power-law non-Newtonian fluid

Poiseuille's law in a slightly tapered tube

Hagen–Poiseuille equation calculator

[hist-1] Sutera, Salvatore P.; Skalak, Richard (1993). "The History of Poiseuille's Law". Annual Review of Fluid Mechanics. 25: 1–19. Bibcode:1993AnRFM..25....1S. doi:10.1146/annurev.fl.25.010193.000245..mw-parser-output cite.citationfont-style:inherit.mw-parser-output .citation qquotes:"""""""'""'".mw-parser-output .citation .cs1-lock-free abackground:url("//upload.wikimedia.org/wikipedia/commons/thumb/6/65/Lock-green.svg/9px-Lock-green.svg.png")no-repeat;background-position:right .1em center.mw-parser-output .citation .cs1-lock-limited a,.mw-parser-output .citation .cs1-lock-registration abackground:url("//upload.wikimedia.org/wikipedia/commons/thumb/d/d6/Lock-gray-alt-2.svg/9px-Lock-gray-alt-2.svg.png")no-repeat;background-position:right .1em center.mw-parser-output .citation .cs1-lock-subscription abackground:url("//upload.wikimedia.org/wikipedia/commons/thumb/a/aa/Lock-red-alt-2.svg/9px-Lock-red-alt-2.svg.png")no-repeat;background-position:right .1em center.mw-parser-output .cs1-subscription,.mw-parser-output .cs1-registrationcolor:#555.mw-parser-output .cs1-subscription span,.mw-parser-output .cs1-registration spanborder-bottom:1px dotted;cursor:help.mw-parser-output .cs1-ws-icon abackground:url("//upload.wikimedia.org/wikipedia/commons/thumb/4/4c/Wikisource-logo.svg/12px-Wikisource-logo.svg.png")no-repeat;background-position:right .1em center.mw-parser-output code.cs1-codecolor:inherit;background:inherit;border:inherit;padding:inherit.mw-parser-output .cs1-hidden-errordisplay:none;font-size:100%.mw-parser-output .cs1-visible-errorfont-size:100%.mw-parser-output .cs1-maintdisplay:none;color:#33aa33;margin-left:0.3em.mw-parser-output .cs1-subscription,.mw-parser-output .cs1-registration,.mw-parser-output .cs1-formatfont-size:95%.mw-parser-output .cs1-kern-left,.mw-parser-output .cs1-kern-wl-leftpadding-left:0.2em.mw-parser-output .cs1-kern-right,.mw-parser-output .cs1-kern-wl-rightpadding-right:0.2em

[2] István Szabó, ;;Geschichte der mechanischen Prinzipien und ihrer wichtigsten Anwendungen, Basel: Birkhäuser Verlag, 1979.

[Kirby-3] Kirby, B. J. (2010). Micro- and Nanoscale Fluid Mechanics: Transport in Microfluidic Devices. Cambridge University Press. ISBN 978-0-521-11903-0.

[Bruus-4] Bruus, H. (2007). Theoretical Microfluidics.

[5] "Poiseuille and his law" (PDF). pdfs.semanticscholar.org.

[6] Vogel, Steven (1981). Life in Moving Fluids: The Physical Biology of Flow. PWS Kent Publishers. ISBN 0871507498.

[7] Determinants of blood vessel resistance.

[Batchelor,_George_Keith_2000-8] Batchelor, George Keith. An introduction to fluid dynamics. Cambridge university press, 2000.

[9] Rosenhead, Louis, ed. Laminar boundary layers. Clarendon Press, 1963.

[10] Drazin, Philip G., and Norman Riley. The Navier–Stokes equations: a classification of flows and exact solutions. No. 334. Cambridge University Press, 2006.

[11] Boussinesq, Joseph. "Mémoire sur l’influence des Frottements dans les Mouvements Réguliers des Fluids." J. Math. Pures Appl 13.2 (1868): 377-424.

[12] Proudman, J. "IV. Notes on the motion of viscous liquids in channels." The London, Edinburgh, and Dublin Philosophical Magazine and Journal of Science 28.163 (1914): 30-36.

[13] Samuel Newby Curle and H.J. Davies. Modern Fluid Dynamics. Volume 1, Incompressible Flow, Van Nostrand Reinhold Inc (1971)